The association of blood phenylalanine levels with IQ was meta-analyzed using a hierarchical mixed-effects model, estimated using Markov chain Monte Carlo (MCMC) methods¹. The advantages of using a Bayesian approach to meta-analysis were recognized over a decade ago² and they have been applied extensively ever since^{3, 4, 5, 6, 7, 8, 9, 10}. It allows for straightforward probabilistic inference across studies, and readily combines both fixed and random effects. In contrast to the more indirect measures of inference afforded by classical methods, all inference from Bayesian models is in the form of probability statements that describe the uncertainty in the unknown quantities of interest (θ), given the information at hand (y):

The left side of this equation is the posterior distribution of all unknown parameters in the model, while right side shows that this posterior quantity is the product of a data likelihood and the prior distribution (i.e. before data are observed) of the model. While the use of priors allows for the incorporation of extant information into the analysis, we used uninformative priors on all parameters, allowing the results from the included studies to provide all the evidence.

Using random effects for meta-analysis permits us to abandon the tenuous assumption that the effects across studies are independent and identically distributed. Rather, we view them as exchangeable samples from a “population” of PKU studies. This conditional independence (i.e., conditional on population parameters) assumption avoids either having to combine studies in a single estimate (which assumes they are identical) or keeping them entirely separate (which assumes they are completely different), but rather, allows for some mixture of the two extremes. In contrast, fixed effects models force one of these unlikely extremes. Moreover, the degree to which studies are pooled is dictated by the heterogeneity across studies, rather than via arbitrary weighting factors.

We specified random effects for the intercept and slope parameters of a linear relationship between blood Phe level and IQ. Importantly, this allowed each study to have its own parameters, each sampled from a notional population of parameters. Those with smaller sample sizes were automatically shrunk towards the population means for each parameter, with larger studies influencing the estimate of the population mean more than being influenced by it. In turn, the magnitude of the effect (i.e. slope) was specified partly as a function of a fixed effect for whether measurements of Phe were carried out during the critical period. Hence, the overall model was a hierarchical mixed effects model. Bayesian hierarchical models are very easily estimated using Markov chain Monte Carlo (MCMC) methods¹¹.

The core of the model is a linear relationship between the expected IQ (μ) and Phe (x):

The subscript j[i] denote parameters for study j corresponding to observation i. Hence, both the intercept and slope are allowed to vary by study. Note that by “observation” we refer here not to individuals, but to groups of individuals within a study that share a characteristic. For example, within the same study, one group of individuals might have been measured for Phe in the critical period, and others not; these groups were considered separate observations in this analysis. One study¹² reported a range of Phe measurements, rather than a single value, so we imputed values by randomly sampling at every iteration from a uniform distribution across the reported range.

Though age was included as an additional linear predictor in early versions of the model, it did not appear to be an important covariate, and models in which it was included did not exhibit good convergence. Hence, age was omitted from the final model. We suspect that the important aspects of age might be adequately characterized by the four combinations of historical or concurrent Phe measurement and measurement in or outside the critical period.

The intercept was modeled as a random effect, where each study is assumed to be an exchangeable sample from a population of PKU studies:

The slope of the relationship included a study-level random effect and fixed effects corresponding to whether the Phe measurement was concurrent with the measurement of IQ (an indicator variable):

Finally, the expected value of IQ was used to model the distribution of observed IQ values y_i, with error described by the inverse variance τ

Twelve studies provided only summarized data, with no individual measurements of Phe or IQ. For studies that provided only data summaries, we were unable to estimate the quantities as specified above. Instead, we employed reported correlation coefficients to obtain additional inference regarding the relationship of these variables. Inference regarding the linear relationship (slope) between Phe and IQ can be obtained from the correlation coefficient (ρ), using the Fisher transformation. Here, the hyperbolic function can be used to transform the correlation to a normally-distributed random variable:

where r_j is the reported Pearson correlation from study j, with a standard error that is solely a function of the corresponding sample size (for a Spearman correlation, the standard error is the inverse square root of n-2). This provides a measure of precision for the reported correlations, which in turn becomes a measure of precision for the slope of the relationship between Phe and IQ. The expected value of the slope is obtained in the model by converting ρ using the fundamental relationship:

where s_xj and s_yj are the reported standard deviations of the Phe levels and IQs, respectively, for study j.

The full model structure is illustrated in Figure F-1. Note the distinction between the influence of studies with group-summarized data and that of studies with individual-level data.

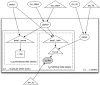
Figure F-1

Directed acyclic graph (DAG) showing the meta-analysis model structure. Note: Unfilled circles represent stochastic nodes, shaded circles represent data, triangles represent deterministic nodes and squares represent factor potentials (arbitrary log-probability (more...)

All stochastic parameters were specified using diffuse prior distributions. For continuous parameters on the real line (e.g. linear model coefficients), a normal distribution with mean zero and precision (inverse-variance) 0.01 was used. For precision parameters, the standard deviation was modeled uniformly on the interval (0, 1000) and then transformed to inverse variance; this provides a better non-informative prior than modeling the precision directly ¹³.

In order to evaluate the effect of particular levels of Phe on the likelihood of cognitive impairment, we chose a threshold value of IQ to bound the definition of impairment. While discretizing a continuous variable into one dichotomous variable is subjective and problematic, we felt that for a standardized measure like IQ, a boundary of one standard deviation below the mean (IQ=85) was a reasonable choice. This threshold value was used to define indicator variables that were set to one if the value of the predicted IQ was below 85 during the current iteration of the MCMC sampler, and zero otherwise. Hence, the total number of ones divided by the number of MCMC iterations represents a posterior probability of observing IQ<85. This corresponds to the integral of the posterior distribution of IQ up to an 85 score. To illustrate the variation of this probability in response to Phe, this probability was calculated for a range of blood Phe levels from 200 to 3000 μmol/L, in increments of 200. This was done for critical period and non-critical period Phe measurement, under both the historical and concurrent measurement models.

This model was coded in PyMC version 2.1¹⁴, which implements several MCMC algorithms for fitting Bayesian hierarchical models. The model was run for one million iterations, with the first 900,000 discarded as a burn-in interval. The remaining sample was thinned by a factor of ten to account for autocorrelation, yielding 10,000 samples for inference. Convergence of the chain was checked through visual inspection of the traces of all parameters, and via the Geweke¹⁵ diagnostic. Posterior predictive checks¹ were performed, which compare data simulated from the posterior distribution to the observed data. This exercise showed no substantial lack of fit for any of the studies included in the dataset.