NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.
Madame Curie Bioscience Database [Internet]. Austin (TX): Landes Bioscience; 2000-2013.
Computer simulations can be used to predict the dynamic behaviour of metabolic pathways and to provide evidence in support of clinical treatments for metabolic disorders. Here, we performed dynamic kinetic simulations of mitochondrial energy metabolism using the E-Cell Simulation Environment. The simulation model was developed as a reconstruction of publicly available kinetic studies on the enzymes of the respiratory chain, the TCA cycle, fatty acid β-oxidation and the inner-membrane metabolite transporters.1Rate equations for the 58 enzymatic reactions and 286 of the 471 kinetic parameters were taken from 36 and 45 articles, respectively. Approximately 80% of the articles that contributed to the kinetic properties of the mitochondrial model have "kinetics" and the enzyme name as their MeSH terms. The published data were mainly obtained from various tissues in five mammals (human, bovine, pig, rabbit and rat). The other kinetic parameters were estimated numerically using a genetic algorithm module of E-Cell to satisfy the Lineweaver-Burk plot of each enzyme. The simulations indicated that increasing coenzyme Q and succinate promotes the total activity of the respiratory chain without affecting other pathways. This result agrees qualitatively with a clinical case report of treatment with coenzyme Q and succinate.2In another case, oxoglutarate supplementation also activated the respiratory chain, but mainly through activation by Complex I. This contrasts with the electron donation through the succinate dehydrogenase complex in the case of coenzyme Q + succinate. These results support the utility of the mitochondrial metabolism model in elucidating action mechanism of clinical treatments.
Background
Computer simulations of metabolic pathways have been employed as a method to predict the dynamic behaviour of metabolic pathways since the 1960s and have recently been revisited in the context of systems biology. In their pioneering work, Chance et al calculated the time evolution of carbon metabolism in ascites tumour cells from numerical integration of 22 rate equations.3While Chance et al employed the law of mass action to approximate the reactions, later metabolic pathway simulations have often been based on kinetic studies on each enzyme. These attempts resulted in simulations on the whole-cell scale, such as the human red blood cell model by Joshi and Palsson.4
Mitochondrial energy metabolism has also been simulated, with a focus on its central role in eukaryotic energy metabolism and the pathology of mitochondrial dysfunction. For example, the respiratory chain was modelled by Korzeniewski and Froncisz5to analyze the control of ATP production. Another example, the TCA cycle of Dictyostelium discoideum, was simulated and analyzed in terms of metabolic control analysis.6However, these previous mitochondrial models simulated groups of pathways one by one, rather than several pathways cooperating in the organelle. We constructed a mitochondrial model that includes the respiratory chain, the TCA cycle, fatty acid β-oxidation and the metabolite transport system at the inner-membrane.1All the rate equations of the model were obtained from published enzyme kinetics. The model is capable of calculating the time evolution of mitochondrial energy metabolism on a whole-organelle scale. Here we have applied this model in two simulation experiments.
Construction of the Model
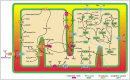
Our mitochondrial model includes 58 enzymatic reactions and 117 metabolites to represent the respiratory chain, the TCA cycle, fatty acid β-oxidation and the inner-membrane metabolite transporters. The inner-membrane metabolite transporters were included to allow simulation of metabolite administration from outside the mitochondrion (Fig. 1). The TCA cycle and the fatty acid β-oxidation process the metabolites transported by the membrane carriers and provide NADH for the respiratory chain.
Kinetic properties of the enzymes, such as Km values and reaction mechanisms, were collected through comprehensive searches of literature databases and enzyme databases such as PubMed (in http://www.ncbi.nlm.nih.gov) and BRENDA (http://www.brenda-enzymes. info). Rate equations for all 58 of the reactions were obtained from 36 articles. Of the 471 total kinetic parameters, 286 were obtained from 45 articles. The other parameters were estimated numerically using the genetic algorithm module to satisfy the Lineweaver-Burk plot of each enzyme.
Ideally, all of the kinetic properties would be derived from experiments on a single cell line under similar conditions in order to faithfully reconstruct the reaction network. However, a homogeneous data set is not available at present. Thus, these data were collected in diverse tissues, mostly obtained from five species of mammal (human, bovine, pig, rabbit and rat).
The data set was implemented as a simulation model of E-Cell, a simulation platform developed to facilitate mixed-mode calculations.7In the standard way of modelling with E-Cell, the mathematical description of a chemical reaction, such as a rate equation, is described in the source file of a small program referred to as "Reactor" ("Process" in version 3), following the grammar and the semantics of the programming language C++. Kinetic parameters and initial metabolite concentrations are described in the "Rulefile", which determines the reaction network and initial condition of the model. To extend the model, the user has only to add Reactors and descriptions of initial metabolite concentrations for newly involved reactions and metabolites, respectively. This feature of E-Cell allows facile integration of independently constructed models. For example, the mitochondrial model is reusable as a module for the simulation of eukaryotic cell metabolism. In the mitochondrial model, the metabolites and enzymes were assigned to one of five compartments: matrix, inner-membrane, outer-membrane, inter-membrane space and cytosol.
PubMed provides a system of keywords called MeSH (Medical Subject Headings), which are embedded in all references included in the database. PubMed users are able to find articles by combining MeSH terms. The search efficiency of comprehensive literature searches is improved when the pattern of MeSH terms embedded in the "HIT" articles (the articles from which the kinetic properties of the mitochondrial model were obtained) is clear. Table 3shows that "kinetics", the enzyme name and the substrate name are the MeSH terms involved in "HIT" articles in most cases. Combining these three keywords made the identification of published articles on kinetics more efficient. For example, "kinetics AND enzyme name" and "kinetics AND substrate name" cover 81% and 74% of the useful articles, respectively.
Table 1.
Abbreviations of the compound names (A-N).
Table 2.
Abbreviations of the compound names (O-).
Table 3.
The pattern of MeSH terms embeedded in the "HIT" articles. "Kinetics and enzyme name" and "kinetics and substrate name" acounted for 81% and 74% of the "HIT" articles, respectively.
Simulation Results
The dynamic behaviour of the metabolic pathway was calculated by the numerical integration of the rate equations programmed into the Reactors, employing the fourth-order Runge-Kutta method implemented in E-Cell. Simulated time courses of enzyme activities and metabolite concentrations are observable by means of a graphical interface named "TracerWindow". Another interface, "SubstanceWindow", allows users to increase or decrease metabolite concentrations while running simulations.
Simulation Experiment 1
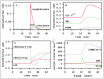
Clinically, several metabolites are widely administered to patients with mitochondrial disorders.8,9The rationales for these metabolic treatments, however, are still unclear in many cases. In our previous study,1we showed the example that increasing coenzyme Q and succinate supplies sufficient electrons to the respiratory chain through the succinate dehydrogenase complex. The evidence supporting this conclusion is presented in Fig. 2: increasing coenzyme Q and succinate results in higher reduction of cytochrome c (Fig. 2A) and activation of the succinate dehydrogenase complex and subsequent respiratory enzymes (SDH, Complex III, IV in Fig. 2B).
In this study, we also examined the effect of this metabolic treatment on the peripheral pathways. Figure 2C,D are time courses of the metabolite concentrations and the enzyme activities of the pathways around coenzyme Q and succinate. No significant concentration change was observed in metabolites such as fumarate, malate and citrate (Fum, Mal and Cit in Fig. 2Crespectively), which are within a few enzyme steps of succinate. Similarly, the enzyme activities of the peripheral pathway were not influenced by coenzyme Q and succinate with the exception of fumarase (FM in Fig. 2D), which is adjacent to succinate dehydrogenase complex in the TCA cycle.
Simulation Experiment 2
In a second simulation, we administered 0.15 mM oxoglutarate to the matrix in a quasi-steady-state. Oxoglutarate increased the activity of one of the respiratory enzymes (Complex I in Fig. 3D) and the concentration of reduced electron transporters (Fig. 3B), ATP (Fig. 3C) and other metabolites such as succinate and 16Acyl-CoA (Fig. 3Aand Fig. 3C, respectively). Of all the enzymes that catalyze reactions in which oxoglutarate is a substrate or a product, aspartate transaminase showed the highest activity, 40-fold greater than that of the oxoglutarate dehydrogenase complex, the second largest.
Discussion
Modelling
Our model was based on published kinetic equations. By extracting a pattern of MeSH terms we were able to construct a more efficient literature-based model and to comprehensively detect a suitable number of papers for kinetic modelling. However, the kinetic properties of enzymes are not being characterised as actively now as in the 1960-70s. Thus, literature-based modelling will be confronted with the practical obstacle that enzymes of interest that have not already been studied might never be examined. To overcome this bottleneck for the simulation of larger pathways, novel methods for comprehensive and high-throughput characterisation of kinetic properties of enzymes will be necessary. A solution to this problem is discussed in reference 10.
Simulation Experiment 1
We found an increase in the total activity of the respiratory chain following an increase in coenzyme Q + succinate, which is qualitatively in agreement with the report of successful clinical treatment with coenzyme Q + succinate.2The simulated time courses suggest a hypothetical rationale for this metabolic treatment: the increase of succinate promotes the respiratory chain by electron donation through the succinate dehydrogenase complex. The activation of the succinate dehydrogenase complex compensated for a decrease in the Complex I activity. The influence of the coenzyme Q + succinate supplementation was observed specifically in the respiratory chain.
Simulation Experiment 2
The activity of the total respiratory chain also increased in Simulation experiment 2; however, the mechanism of the activation was different from that of Simulation experiment 1. The activation of Complex I (Fig. 3D) indicates that NADH oxidation by Complex I is the primary electron donor to the respiratory chain in the condition of Simulation experiment 2, while electrons were mainly supplied through the succinate dehydrogenase complex in Simulation experiment 1.
Another difference between Simulation experiments 1 and 2 is that the oxoglutarate in Simulation experiment 2 affected broader pathways than the coenzyme Q + succinate in Simulation 1. The administration of oxoglutarate influenced metabolite concentrations in the TCA cycle and fatty acid β-oxidation, while the effect of coenzyme Q + succinate was observed specifically around the respiratory chain.
Conclusion
As shown above, simulation studies of metabolic pathways are capable of deriving hypotheses about the dynamics of metabolite concentrations and enzyme activities. However, validation by wet experiments will be required for a more realistic simulation of mitochondria.
At present, there are experimentally observable variables that can be used to check the consistency of the model. Robinson et al reported a method for the quantitative measurement of ATP production of mitochondria using a luminometer.11With this method, it is possible to compare mitochondrial ATP production in vivo and in silico. Moreover, recent advancements in metabolome measurement will facilitate not only the quantification of ATP production but also the comprehensive profiling of intracellular/organellar metabolite concentration.12In cases where only qualitative results are necessary, staining of cytochrome c oxidase can be used to provide qualitative measurements of the enzyme activity. Revision of the mitochondrial model after these experimental validations will provide a more realistic prediction of mitochondrial energy metabolism.
Reference
- 1.
- Yugi K, Tomita M. A general computational model of mitochondrial metabolism. Bioinformatics. 2004;20:1795–1796. [PubMed: 14962921]
- 2.
- Shoffner JM, et al. Spontaneous Kearns-Sayre/chronic external ophthalmoplegia plus syndrome associated with a mitochondrial DNA deletion: a slip-replication model and metabolic therapy. Proc Natl Acad Sci USA. 1989;86:7952–7956. [PMC free article: PMC298190] [PubMed: 2554297]
- 3.
- Chance B, Garfinkel D, Higgins J, et al. Metabolic control mechanisms V: A solution for the equations representing interaction between glycolysis and respiration in ascites tumor cells. J Biol Chem. 1960;235:2426–2439. [PubMed: 13692276]
- 4.
- Joshi A, Palsson BO. Metabolic dynamics in the human red cell: Part I A comprehensive kinetic model. J Theor Biol. 1989;141:515–528. [PubMed: 2630803]
- 5.
- Korzeniewski B, Froncisz W. A dynamic model of mitochondrial respiration. Stud Biophys. 1989;132:173–187.
- 6.
- Wright BE, Butler MH, Albe KR. Systems analysis of the tricarboxylic acid cycle in dictyostelium discoideum. I. The basis for model construction. J Biol Chem. 1992;267:3101–3105. [PubMed: 1737766]
- 7.
- Takahashi K, et al. Computational challenges in cell simulation. IEEE Intelligent Systems. 2002;17:64–71.
- 8.
- Przyrembel H. Therapy of mitochondrial disorders. J Inherit Metab Dis. 1987;10:129–146. [PubMed: 3119936]
- 9.
- Luft R. The development of mitochondrial medicine. Proc Natl Acad Sci USA. 1994;91:8731–8738. [PMC free article: PMC44681] [PubMed: 8090715]
- 10.
- Yugi K, Nakayama Y, Kinoshita A, et al. Hybrid dynamic/static method for large-scale simulation of metabolism. Theoretical Biology and Medical Modelling. 2005;2:42. [PMC free article: PMC1262783] [PubMed: 16202166]
- 11.
- Robinson BH, et al. The use of skin fibroblast cultures in the detection of respiratory chain defects in patients with lacticacidemia. Pediatr Res. 1990;28:549–555. [PubMed: 2175027]
- 12.
- Soga T, et al. Pressure-assisted capillary electrophoresis electrospray ionization mass spectrometry for analysis of multivalent anions. Anal Chem. 2002;74:6224–6229. [PubMed: 12510742]
- 13.
- Barden RE, Fung CH, Utter MF, et al. Pyruvate carboxylase from chicken liver. J Biol Chem. 1972;247:1323–1333. [PubMed: 5010071]
- 14.
- Beckmann JD, Frerman FE. Reaction of electron transfer flavoprotein with electron-transfer flavoprotein-ubiquinone oxidoreductase. Biochemistry. 1985;24:3922–3925. [PubMed: 2996585]
- 15.
- Crow KE, Braggins TJ, Hardman MJ. Human liver cytosolic malate dehydrogenase: purification, kinetic properties and role in ethanol metabolism. Arch Biochem Biophys. 1983;225:621–629. [PubMed: 6625603]
- 16.
- Davisson VJ, Schulz AR. The purification and steady-state kinetic behaviour of rabbit heart mitochondrial NAD(P)+ malic enzyme. Biochem J. 1985;225:335–342. [PMC free article: PMC1144595] [PubMed: 3977837]
- 17.
- De Rosa G, Burk TL, Swick RW. Isolation and characterization of mitochondrial alanine aminotransferase from porcine tissue. Biochim Biophys Acta. 1979;567:116–124. [PubMed: 454616]
- 18.
- Dierks T, Kramer R. Asymmetric orientation of the reconstituted aspartate/glutamete carrier from mitochondria. Biochim Biophys Acta. 1988;937:112–126. [PubMed: 3334841]
- 19.
- Fato R, et al. Steady-state kinetics of the reduction of coenzyme Q analogs by complex I (NADH:ubiquinone oxidoreductase) in bovine heart mitochondria and submitochondrial particles. Biochemistry. 1996;35:2705–2716. [PubMed: 8611577]
- 20.
- Grivennikova VG, Gavrikova EV, Timoshin AA, et al. Fumarate reductase activity of bovine heart succinate-ubiquinone reductase. new assay system and overall properties of the reaction. Biochim Biophys Acta. 1993;1140:282–292. [PubMed: 8417779]
- 21.
- Guarriero-Bobyleva V, Masini A, Volpi-Becchi MA, et al. Kinetic studies of cytoplasmic and mitochondrial aconitate hydratases from rat liver. Ital J Biochem. 1978;27:287–299. [PubMed: 755796]
- 22.
- Hamada M, et al. A kinetic study of the alpha-keto acid dehydrogenase complexes from pig heart mitochondria. J Biochem (Tokyo). 1975;77:1047–1056. [PubMed: 169232]
- 23.
- Indiveri C, Dierks T, Kramer R, et al. Reaction mechanism of the reconstituted oxoglutarate carrier from bovine heart mitochondria. Eur J Biochem. 1991;198:339–347. [PubMed: 2040299]
- 24.
- Indiveri C, Tonazzi A, Prezioso G, et al. Kinetic characterization of the reconstituted carnitine carrier from rat liver mitochondria. Biochim Biophys Acta. 1991;1065:231–238. [PubMed: 2059655]
- 25.
- Indiveri C, Tonazzi A, Palmieri F. The reconstituted carnitine carrier from rat liver mitochondria: evidence for a transport mechanism different from that of the other mitochondrial translocators. Biochim Biophys Acta. 1994;1189:65–73. [PubMed: 8305461]
- 26.
- Kholodenko BN. Kinetic models of coupling between H+ and Na(+)-translocation and ATP synthesis/hydrolysis by FoF1-ATPases: can a cell utilize both delta mu H+ and delta mu Na+ for ATP synthesis under in vivo conditions using the same enzyme? J Bioenerg Biomembr. 1993;25:285–295. [PubMed: 8394322]
- 27.
- Kramer R, Klingenberg M. Electrophoretic control of reconstituted adenine nucleotide translocation. Biochemistry. 1982;21:1082–1089. [PubMed: 6280754]
- 28.
- Kubota T, Yoshikawa S, Matsubara H. Kinetic mechanism of beef heart ubiquinol: cytochrome c oxidoreducase. J Biochem (Tokyo). 1992;111:91–98. [PubMed: 1318882]
- 29.
- Malmstrom BG, Andreasson LE. The steady-state rate equation for cytochrome c oxidase based on a minimal kinetic scheme. J Inorg Biochem. 1985;23:233–242. [PubMed: 2991462]
- 30.
- Mann WR, Yan B, Dragland CJ, et al. Kinetic, circular dichroism and fluorescence studies on heterologously expressed carnitine palmitoyltransferase II. J Enzym Inhib. 1995;9:303–308. [PubMed: 8598540]
- 31.
- Matsuoka Y, Srere PA. Kinetic studies of citrate synthase from rat kidney and rat brain. J Biol Chem. 1973;248:8022–8030. [PubMed: 4201777]
- 32.
- McKean MC, Frerman FE, Mielke DM. General acyl-CoA dehydrogenase frome pig liver. J Biol Chem. 1979;254:2730–2735. [PubMed: 429316]
- 33.
- Miyazawa S, Furuta S, Osumi T, et al. Properties of peroxisomal 3-ketoacyl-CoA thiolase from rat liver. J Biochem (Tokyo). 1981;90:511–519. [PubMed: 6117552]
- 34.
- Mukherjee A, Srere PA. Purification of and mechanism studies on citrate synthase. J Biol Chem. 1976;251:1476–1480. [PubMed: 1254579]
- 35.
- Plaut GWE, Schramm VL, Aogaichi T. Action of magnesium ion on diphosphopyridine nucleotide-linked isocitrate dehydrogenase from bovine heart. J Biol Chem. 1974;249:848–1856. [PubMed: 4361827]
- 36.
- Ramsay RR, Derrick JP, Friend AS, et al. Purification and properties of the soluble carnitine palmitoyltransferase from bovine liver mitochondria. Biochem J. 1987;244:271–278. [PMC free article: PMC1147987] [PubMed: 3663121]
- 37.
- Sluse FE, et al. Kinetic study of the aspartate/glutamate carrier in intact rat heart mitochondria and comparison with a reconstituted system. Biochim Biophys Acta. 1991;1058:329–338. [PubMed: 2065061]
- 38.
- Stappen R, Kramer R. Kinetic mechanism of phosphate/phosphate and phosphate/OH- antiports catalyzed by reconstituted phosphate carrier from beef heart mitochondria. J Biol Chem. 1994;269:11240–11246. [PubMed: 8157653]
- 39.
- Yang SY, Schulz H. Kinetics of coupled enzyme reactions. Biochemistry. 1987;26:5579–5584. [PubMed: 3676269]
- 40.
- Velick SF, Vavra J. A kinetic and equilibrium analysis of the glutamic oxaloacetate transaminase mechanism. J Biol Chem. 1962;237:2109–2122. [PubMed: 13925259]
- 41.
- Henson CP, Cleland WW. Kinetic studies of glutamic oxaloacetic transaminase isozymes. Biochemistry. 1964;3:338–345. [PubMed: 14155095]
- 42.
- Bisaccia F, De Palma A, Dierks T, et al. Reaction mechanism of the reconstituted tricarboxylate carrier from rat liver mitochondria. Biochim Biophys Acta. 1993;1142:139–145. [PubMed: 8457581]
- 43.
- Matsuno-Yagi A, Hatefi Y. Studies on the mechanism of oxidative phosphorylation: catalytic site cooperativity in ATP synthesis. J Biol Chem. 1985;260:14424–14427. [PubMed: 4055778]
- 44.
- Woeltje KF, Kuwajima M, Foster DW, et al. Characterization of the mitochondrial carnitine palmitoyltransferase enzyme system. J Biol Chem. 1987;262:9822–9827. [PubMed: 3597442]
- 45.
- Shepherd D, Garland PB. The kinetic properties of citrate synthase from rat liver mitochondria. Biochem J. 1969;114:597–610. [PMC free article: PMC1184933] [PubMed: 5820645]
- 46.
- Indiveri C, Prezioso G, Dierks T, et al. Kinetic characterization of the reconstituted dicarboxylate carrier from mitochondria: a four-binding-site sequential transport system. Biochim Biophys Acta. 1993;1143:310–318. [PubMed: 8329439]
- 47.
- Hill RL, Teipel JW. The Enzymes volume V in: Boyer PD. Ed. New York and London: Academic Press. 1970:539–571.
- 48.
- Ehrlich RS, Hayman S, Ramachandran N, et al. F Re-evaluation of molecular weight of pig heart NAD-specific isocitrate dehydrogenase. J Biol Chem. 1981;256:10560–10564. [PubMed: 7287723]
- 49.
- Londesborough JC, Dalziel K. Pyridine nucleotide dependent dehydrogenases. In: Sund H, ed. New York: Springer-Verlag. 1970:315–324.
- 50.
- Colomb MG, Cheruy A, Vignais PV. Nucleoside diphosphatekinase from beef heart mitochondria: purification and properties. Biochemistry. 1969;8:1926–1939. [PubMed: 5785215]
- 51.
- Garces E, Cleland WW. Kinetic studies of yeast nucleoside diphosphate kinase. Biochemistry. 1969;8:633–640. [PubMed: 5793714]
- 52.
- Cleland WW. Derivation of rate equations of multisite ping-pong mechanisms with ping-pong reactions at one or more sites. J Biol Chem. 1973;248:8353–8355. [PubMed: 4762915]
- 53.
- Kiselevsky YV, Ostrovtsova SA, Strumilo SA. Kinetic characterization of the pyruvate and oxoglutarate dehydrogenase complexes from human heart. Acta Biochim Pol. 1990;37:135–139. [PubMed: 2087902]
- 54.
- Heckert LL, Butler MH, Reimers JM, et al. Purification and characterization of the 2-oxoglutarate dehydrogenase complex from Dictyostelium discoideum. J Gen Microbiol. 1989;135:155–161. [PubMed: 2778429]
- 55.
- Nalecz KA. Molecular biology of mitochondrial transport systems. In: Forte M, Colombini M, eds. Springer-Verlag Berlin Heidelberg. 1994:67–79.
- 56.
- Capuano F, Di Paola M, Azzi A, et al. The monocarboxylate carrier from rat liver mitochondria: purification and kinetic characterization in a reconstituted system. FEBS Lett. 1990;261:39–42. [PubMed: 2307234]
- 57.
- Cha S, Parks Jr. RE. Succinic thiokinase II. kinetic studies: Initial velocity, product inhibition and effect of arsenate. J Biol Chem. 1964;239:1968–1977. [PubMed: 14213385]
Appendix A
Supporting Table 1.Initial concentrations of metabolites and enzymes
| Enzyme | Localisation | Number of Molecules |
|---|---|---|
| Complex-I | MT-IM | 1000 |
| Complex-III | MT-IM | 3000 |
| Complex-IV | MT-IM | 7000 |
| Complex-V | MT-IM | 900 |
| CS | MATRIX | 100 |
| ACO | MATRIX | 100 |
| IDHa | MATRIX | 100 |
| IDHb | MATRIX | 100 |
| OGDC | MATRIX | 100 |
| SCS | MATRIX | 100 |
| SDH | MT-IM | 100 |
| FM | MATRIX | 100 |
| MDH | MATRIX | 100 |
| AlaTA | MATRIX | 100 |
| AspTA | MATRIX | 100 |
| NDK | MATRIX | 100 |
| PDC | MATRIX | 100 |
| PC | MATRIX | 100 |
| CPT-I | MT-OM | 100 |
| CAC | MT-IM | 100 |
| ACD | MT-IM | 100 |
| ECH | MT-IM | 100 |
| HCD | MT-IM | 100 |
| OCT | MT-IM | 100 |
| ETF-QO | MT-IM | 100 |
| AAC | MT-IM | 1000 |
| AGC | MT-IM | 1000 |
| PiC | MT-IM | 1000 |
| PYC | MT-IM | 1000 |
| OGC | MT-IM | 1000 |
| DIC | MT-IM | 1000 |
| CIC | MT-IM | 1000 |
| Compound | Localisation | Concentration |
| Q | MT-IMS | 0.26 mM |
| QH2 | MT-IMS | 28 μM |
| cyt-c3+ | MT-IMS | 3 μW |
| cyt-c2+ | MT-IMS | 0.11 m M |
| H+ | MT-IMS | 1 μM |
| H+ | MATRIX | 10 nM |
| Cit | MT-IMS | 0.42 mM |
| Cit | MATRIX | 0.42 mM |
| IsoCit | MATRIX | 0.42 mM |
| OG | MT-IMS | 21 μM |
| OG | MATRIX | 21 μM |
| SCoA | MATRIX | 0.29 mM |
| Suc | MATRIX | 2.95 mM |
| Fum | MATRIX | 65.00 μM |
| Mal | MT-IMS | 0.50 mM |
| Mal | MATRIX | 0.50 mM |
| OXA | MATRIX | 4.00 μM |
| Asp | MATRIX | 1.14 mM |
| Asp | MT-IMS | 1.14 mM |
| Glu | MATRIX | 3.03 mM |
| Glu | MT-IMS | 3.03 mM |
| Ala | MATRIX | 3.44 mM |
| Pyr | MT-IMS | 0.10 mM |
| Pyr | MATRIX | 0.10 mM |
| CoA | MT-IMS | 0.27 mM |
| CoA | MATRIX | 0.27 mM |
| Acetyi-CoA | MATRIX | 30.00 μM |
| NADH | MATRIX | 72.00 μM |
| NAD+ | MATRIX | 0.17 m M |
| NADPH | MATRIX | 72.00 μM |
| NADP+ | MATRIX | 0.17 m M |
| CO2 | MATRIX | 1.63 m M |
| ATP | MT-IMS | 4.50 mM |
| ATP | MATRIX | 4.50 mM |
| ADP | MT-IMS | 0.45 mM |
| ADP | MATRIX | 0.45 mM |
| GTP | MATRIX | 4.50 mM |
| GDP | MATRIX | 0.45 mM |
| Pi | MT-IMS | 4.00 mM |
| Pi | MATRIX | 4.00 mM |
| Car | MT-IMS | 0.20 mM |
| Car | MATRIX | 0.95 mM |
| PalCar | MT-IMS | 0.60 mM |
| PalCar | MATRIX | 12.00 μM |
| ETFred | MATRIX | 0.31 μM |
| ETFox | MATRIX | 0.32 μM |
| 16Acyl-CoA | MATRIX | 39.00 μM |
| 16Enoyl-CoA | MATRIX | 17.00 μM |
| 16Hydroxyacyl-CoA | MATRIX | 12.00 μM |
| 160xoacyl-CoA | MATRIX | 1.10 μM |
| 14Acyl-CoA | MATRIX | 39.00 μM |
| 14Enoyl-CoA | MATRIX | 17.00 μM |
| 14 Hydroxyacyl-CoA | MATRIX | 12.00 μM |
| 140xoacyl-CoA | MATRIX | 1.10 μM |
| 12Acyl-CoA | MATRIX | 87.00 μM |
| 12Enoyl-CoA | MATRIX | 17.00 μM |
| 12Hydroxyacyl-CoA | MATRIX | 12.00 μM |
| 120xoacyl-CoA | MATRIX | 1.30 μM |
| 10Acyl-CoA | MATRIX | 87.00 μM |
| 10Enoyl-CoA | MATRIX | 17.00 μM |
| 10Hydroxyacyl-CoA | MATRIX | 12.00 μM |
| 10Oxoacyl-CoA | MATRIX | 2.10 μM |
| 3Acyl-CoA | MATRIX | 87.00 μM |
| 8Enoyl-CoA | MATRIX | 17.00 μM |
| 8Hydroxyacyl-CoA | MATRIX | 12.00 μM |
| 8Oxoacyl-CoA | MATRIX | 3.20 μM |
| Compound | Localisation | Concentration |
| 6Acyl-CoA | MATRIX | 87.00 μM |
| 6Enoyl-CoA | MATRIX | 17.00 μM |
| 6Hydroxyacyl-CoA | MATRIX | 12.00 μM |
| 60xoacyl-CoA | MATRIX | 6.70 μM |
| 4Acyl-CoA | MATRIX | 87.00 μM |
| 4Enoyl-CoA | MATRIX | 17.00 μM |
| 4Hydroxyacyl-CoA | MATRIX | 12.00 μM |
| Aceloacetyl-CoA | MATRIX | 12.40 μM |
Supporting Table 2.Steady-state amounts of metabolites and enzymes
| Compound | Localisation | Number of Molecules |
|---|---|---|
| Q | MT-IMS | 77547 |
| QH2 | MT-IMS | 500 |
| cyt-c3+ | MT-IMS | 29624 |
| cyt-c2+ | MT-IMS | 999 |
| H+ | MT-IMS | 3 |
| H+ | MATRIX | 3 |
| Cit | MT-IMS | 1265 |
| Cit | MATRIX | 583455 |
| IsoCit | MATRIX | 74758 |
| OG | MT-IMS | 63 |
| OG | MATRIX | 424 |
| SCoA | MATRIX | 32 |
| Suc | MATRIX | 1133 |
| Fum | MATRIX | 231567 |
| Mal | MT-IMS | 1506 |
| Mal | MATRIX | 1028383 |
| OXA | MATRIX | 302 |
| Asp | MATRIX | 244090 |
| Asp | MT-IMS | 3433 |
| Glu | MATRIX | 801482 |
| Glu | MT-IMS | 9124 |
| Ala | MATRIX | 1016709 |
| Pyr | MT-IMS | 27777 |
| Pyr | MATRIX | 309 |
| CoA | MT-IMS | 700 |
| CoA | MATRIX | 286 |
| Acetyl-CoA | MATRIX | 104498 |
| NADH | MATRIX | 3672 |
| NAD+ | MATRIX | 61909 |
| NADPH | MATRIX | 7508 |
| NADP + | MATRIX | 58073 |
| CO2 | MATRIX | 42631671 |
| ATP | MT-IMS | 13550 |
| ATP | MATRIX | 180 |
| ADP | MT-IMS | 1355 |
| ADP | MATRIX | 121948 |
| GTP | MATRIX | 2579 |
| GDP | MATRIX | 1338852 |
| Pi | MT-IMS | 12044 |
| Pi | MATRIX | 2507395 |
| Car | MT-IMS | 602 |
| Car | MATRIX | 47418 |
| PalCar | MT-MS | 1807 |
| PalCar | MATRIX | 213280 |
| 16Acyl-CoA | MT-MS | 117 |
| ETFred | MATRIX | 89 |
| ETFox | MATRIX | 82 |
| 16Acyl-CoA | MATRIX | 331 |
| 16Enoyl-CoA | MATRIX | 698 |
| 16Hydroxyacyl-CoA | MATRIX | 3 |
| 16Oxoacyl-CoA | MATRIX | 769 |
| 14Acyl-CoA | MATRIX | 331 |
| 14Enoyl-CoA | MATRIX | 699 |
| 14Hydroxyacyl-CoA | MATRIX | 3 |
| 14Oxoacyl-CoA | MATRIX | 771 |
| 12Acyl-CoA | MATRIX | 330 |
| 12Enoyl-CoA | MATRIX | 700 |
| 12Hydroxyacyl-CoA | MATRIX | 2 |
| 12Oxoacyl-CoA | MATRIX | 763 |
| 10Acyl-CoA | MATRIX | 331 |
| 10Enoyl-CoA | MATRIX | 700 |
| 10Hydroxyacyl-CoA | MATRIX | 2 |
| 10Oxoacyl-CoA | MATRIX | 762 |
| BAcyl-CoA | MATRIX | 332 |
| 8Enoyl-CoA | MATRIX | 701 |
| 8Hydroxyacyl-CoA | MATRIX | 2 |
| 80xoacyl-CoA | MATRIX | 763 |
| 6Acyl-CoA | MATRIX | 332 |
| 6Enoyl-CoA | MATRIX | 701 |
| 6Hydroxyacyl-CoA | MATRIX | 3 |
| 6Oxoacyl-CoA | MA | 764 |
| 4Acyl-CoA | MATRIX | 331 |
| 4Enoyl-CoA | MATRIX | 702 |
| 4Hydroxyacyl-CoA | MATRIX | 2 |
| Acetoacetyl-CoA | MATRIX | 239686 |
Supporting Table 3.Parameter classification
| Class | Defnition | Example |
|---|---|---|
| Class 0 | Found in the literature | Km = 2.3 mM |
| Class 1 | Estimated around the values in the literature | Km = 2.3 mM → Km = 2.6 mM |
| Class 2 | Estimated around the values of analogous metabolites | KmATP = 2.3 mM → 0 < KmGTP <3.0 mM |
| Class 3 | Estimated arbitrarily | ? < k < ?→ k = 1.2 x 109sec-1 |
Supporting Table 4.The kinetic properties of AAC
| Reaction | ATP(MAT) → ATP(IMS), ADP(MAT) → ADP(IMS) | ||
| Mechanism | See ref. 27 | ||
| Rate equation | Eqn. 1 | ||
| Species, organ | Rat heart mitochondria | ||
| Parameter | Class | notice | |
| kf0 | 0.9 | Class 0 | Velocity model (mp = 0, kf0 = kr0) |
| kr0 | 0.9 | Class 0 | Velocity model (mp = 0) |
| Normalize | 2.21 | Class 0 | Normalizing factor of kf0 and kr0 |
| Kd1 | 5.9 x 10-4 | Class 3 | Kd1 → Kd velocity model, Kd1 = Kd2 |
| Kd2 | 5.9 x 10-4 | Class 3 | Kd1 → Kd’ Kd is not effected by the membrane potentia |
| Cf | 3.30 | Class 0 | Kf0 x exp(Cf x ψ) = kf(ψ) |
| Cf | -3.34 | Class 0 | Kr0 x exp(Cr x ψ) = kr(ψ) |
| T | 310.0 K | – | Absolute temperature |
Source of parameter estimation: Figure 2(B) V D→ (Δψ = 0mV, 180mV) in reference 27.
Supporting Table 5.The kinetic properties of ACD
| Reaction | Acyl-CoA + ETFox ⇔ Enoyl-CoA + ETFred | ||
| Mechanism | Ordered Bi Bi32 | ||
| Rate equation | |||
| Species, organ | Pig liver mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmS1 | 39 x 10-6 | Class 0 | Ref. 32 Table 1 |
| KmS2 | 0.12 x 10-6 | Class 0 | |
| KmP1 | 1.08 x 10-6 | Class 2 | |
| KmP2 | 2.42 x 10-5 | Class 2 | |
| KiS1 | 76 x 10-6 | Class 0 | |
| KiS2 | 0.24 x 10-6 | Class 0 | |
| K iP 1 | 7.53 x 10-5 | Class 2 | |
| KiP2 | 1.19 x 10-5 | Class 2 | |
| Keq | 8.99 | Class 3 | |
| KcF | 2.18 | Class 0 | |
| KcR | 0.30 | Class 2 | |
Source for parameter estimation: reference 32.
Supporting Table 6.The kinetic properties of ACO
| Reaction | Cit ⇔ IsoCit | ||
| Mechanism | Uni uni reversible21 | ||
| Rate equation | |||
| Species, organ | Rat liver mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| Ks | 0.50 x 10 3 | Class 0 | |
| Kp | 0.11 x 10-3 | Class 0 | |
| KcF | 20.47 | Class 0 | Calculated from the graph |
| KcR | 31.44 | Class 0 | Calculated from the graph |
Supporting Table 7.The kinetic properties of AGC
| Reaction | Asp(IMS) + Glu (MAT) ⇔ | ||
| Asp(MAT) + Glu(IMS) | |||
| Mechanism | Rapid equilibrium | ||
| Random Bi Bi37 | |||
| Rate equation | |||
| Species | Rat heart mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KiS1 | 80 x 10-6 | Class 0 | Ref. 18 |
| KiS2 | 3.2 x 10-3 | Class 0 | Ref. 18 |
| KiP1 | 180 x 10-6 | Class 0 | Ref. 18 |
| KiP2 | 2.8 x 10-3 | Class 0 | Ref. 18 |
| KcF | 10.0 | Class 3 | |
| KcR | 10.0 | Class 3 | |
| Alpha | 1.0 | Class 0 | |
| Beta | 1.0 | Class 0 | |
| Gamma | 1.0 | Class 0 | |
| Delta | 1.0 | Class 0 | |
Supporting Table 8.The kinetic properties of AlaTA
| Reaction | Ala + OG ⇔ Glu + Pyr | ||
| Mechanism | Ping-pong Bi Bi17 | ||
| Rate equation | |||
| Species, organ | Pig liver | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmS1 | 0.002 | Class 0 | |
| KmS2 | 0.0004 | Class 0 | |
| KmP1 | 0.032 | Class 0 | |
| KmP2 | 0.0004 | Class 0 | |
| KiS1 | 0.0087 | Class 2 | KiP2 |
| KiP2 | 0.012 | Class 0 | |
| Keq | 0.69 | Class 2 | 0.16, AspTA |
| At MW = 78000 | |||
| KcF | 337 | Class 0 | Activity = 210 micromol/min/mg |
| KcR | 0.15 | Class 3 | |
Source for parameter estimation: Figure 3 with 5 mM glutamate in reference 17.
Supporting Table 9.The kinetic properties of AspTA
| Reaction | Asp + OG ⇔ OxA + Glu | ||
| Mechanism | Ping-pong Bi Bi-40,41 | ||
| Rate equation | |||
| Species, organ | Pig heart | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmS1 | 0.9 x 10-3 | Class 0 | Ref. 40, Table II |
| KmS2 | 0.1 x 10-3 | Class 0 | Ref. 40, Table II |
| KmP1 | 0.04 x 10-3 | Class 0 | Ref. 40, Table II |
| KmP2 | 4 x 10-3 | Class 0 | Ref. 40, Table II |
| KiS1 | 2 x 10-3 | Class 0 | Ref. 40, Table II |
| KiP2 | 8.3 x 10-3 | Class 0 | Ref. 40, Table II |
| Keq | 6.2 | Class 0 | |
| KcF | 300 | Class 0 | |
| KcR | 1000 | Class 0 | From k4 and k 10 |
Supporting Table 10.The kinetic properties of CAC
| Reaction | PalCar(IMS) + Car(MAT) ⇔ PalCar(MAT) + Car(IMS) | ||
| Mechanism | Ping-pong Bi Bi25 | ||
| Rate equation | |||
| Species | Rat liver mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmS1 | 0.6 x 10-3 | Class 0 | Ref. 25 |
| KmS2 | 9.4 x 10-3 | Class 0 | Ref. 25 |
| KmP1 | 43.4 x10-6 | Class 1 | 11.6 x 10-6, the value of Car/Car reaction |
| KmP2 | 0.4 x 10-3 | Class 1 | 1.2 x 10-3, the value of Car/Car reaction |
| KiS1 | 8.7x10-6 | Class 1 | 5.1 x 10-6, ref. 24 |
| KiP2 | 250x10-6 | Class 1 | 510 x 10-6, ref. 24 |
| Keq | 243.3 | Class 3 | |
| KcF | 1.22 | Class 2 | |
| KcR | 1.08 | Class 1 | 0.92, ref. 24 |
Source for parameter estimation: Figure 4 with 13 mM acetylcarnitine in reference 24.
Supporting Table 11.The kinetic properties of CIC
| Reaction | Cit(IMS) + Mal(MAT) ⇔ Cit(MAT) + Mal(IMS) | ||
| Mechanism | Rapid equilibrium random Bi Bi42 | ||
| Rate equation | |||
| Species | Rat liver mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KiS1 | 1.3 x10-4 | Class 2 | |
| KiS2 | 4.4 x 10-4 | Class 2 | |
| KiP1 | 3.3 x10-4 | Class 0 | |
| KiP2 | 4.18 x10-5 | Class 0 | |
| KcF | 5.6 | Class 0 | 11.2 mmol/min/g prot. x 30 kDa |
| KcR | 3.5 | Class 1 | KcR = 2.1 (ref. 42, Table II) |
| Alpha | 1.0 | Class 0 | |
| Beta | 1.0 | Class 0 | |
| Gamma | 1.0 | Class 0 | |
| Delta | 1.0 | Class 0 | |
Source for parameter estimation: Figure 1(A) with 0.05 mM citrate, (C) with 0.05 mM malate in reference 42.
Supporting Table 12.The kinetic properties of complex I
| Reaction | NADH + Q + 5H+(MAT) ⇔ NAD++ QH2+ 4H+(IMS) | ||
| Mechanism | Ping-pong Bi Bi19 | ||
| Rate equation | Eqn. 11 | ||
| Species, organ | Bovine heart mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmS1 | 9.2 x 10-6 | Class 0 | |
| KmS2 | 2.6 x 10-4 | Class 0 | |
| KmP1 | 9.9 x 10-6 | Class 2 | |
| KmP2 | 5.9 x 10-5 | Class 2 | |
| KiS1 | 2.1 x 10-8 | Class 0 | KiS1 = 1/Kmin |
| KiP2 | 9.8 x 10-8 | Class 2 | |
| Keq | 407.9 | Class 3 | |
| KcF | 498 | Class 0 | |
| KcR | 229 | Class 2 | |
Source of parameter estimation: Figure 1C with 2.4 μM reduced CoQ2in reference 19.
Supporting Table 13.The kinetic properties of complex III
| Reaction | QH2+ 2cyt c3++ 2H+(MAT) → Q + 2cyt c2++ 4H+(IMS) | ||
| Mechanism | See ref. 28 scheme 3 | ||
| Rate equation | Eqn. 3 | ||
| Species, organ | Bovine heart mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmA | 2.8 x 10-5 | Class 0 | K5 x KcF |
| KmB | 3.0 x 10-6 | Class 0 | K6 x KcF |
| Kb1 | 5.4 x 10-6 | Class 2 | k5/k4, K3 = K4 x Kb1 |
| Kb2 | 5.7 x 10-6 | Class 2 | k10/k9, K1 = K2 x Kb2 |
| Kq1 | 2.8 x 10-6 | Class 2 | k7/k6, K4 = Kq1/ks |
| Kq2 | 1.9 x 10-6 | Class 2 | k12/k11, K2 = K5 x Kq2 |
| K8 | 622.1 | Class 2 | |
| KcF | 426.8 | Class 0 | 1/K7 |
Source for parameter estimation: Figure 6 with 15 μM Q2H2in reference 28.
Supporting Table 14.The kinetic properties of complex IV
|
Reaction Mechanism Rate equation Species, organ |
4cyt c2++ O2+ 8H+(MAT) → 4cyt c3++ 2H2O + 4H+(IMS) Michaelis-menten ref. 29 Eqn. 6 | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| Ks | 110 x10-6 | Class 0 | Value at pH = 7 |
| KcF | 93.5 | Class 0 | Value at pH = 7, d[cyt c2+]/dt x 1/4 |
Supporting Table 15.The kinetic properties of complex V
| Reaction | ADP + Pi + 3H+(IMS) ⇔ ATP + H O + 3H+(MAT) | ||
| Mechanism | See ref. 26 | ||
| Rate equation | Eqn. 3 | ||
| Species, organ | |||
| Parameter | Class | Notice | |
|---|---|---|---|
| Kd | 2.67 x 10-7 | Class 3 | |
| Kp | 9.02 x10-5 | Class 3 | |
| Kt | 4.33 x10-5 | Class 3 | |
| KcF | 14.5 | Class 0 | 2340 nmol/min/mg × 371 kDa |
| Khx | 1.3 x10-4 | Class 3 | |
| Khy | 1.6 × 10-4 | Class 3 | |
| Klt f | 1.35 × 108 | Class 3 | |
| Klt r | 0.00018 | Class 3 | |
| Ax | 0.1 | Class 3 | |
| Ay | 0.6 | Class 3 | |
| Beta | 0.3 | Class 3 | |
| T | 310 | - | |
| Source for parameter estimation: Figure 2 with NADH respiration in reference 43. | |||
Supporting Table 16.The kinetic properties of CPT I
| Reaction | 16Acyl-CoA + Car ⇔ CoA + PalCar | ||
| Mechanism | Rapid equilibrium random Bi Bi36 | ||
| Rate equation | |||
| Species, organ | Bovine liver mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KiS1 | 182 x 10-6 | Class 0 | Ref. 36 |
| KiS2 | 0.82 x10-6 | Class 0 | |
| KiP1 | 6.7 x 10-6 | Class 0 | |
| KiP2 | 21 x10-6 | Class 0 | |
| KcF | 61.4 | Class 0 | |
| KcR | 32.8 | Class 0 | |
| Alpha | 1.0 | Class 0 | |
| Beta | 1.0 | Class 0 | |
| Gamma | 1.0 | Class 0 | |
| Delta | 1.0 | Class 0 | |
Supporting Table 17.The kinetic properties of CPT II
| Reaction | CoA + PalCar ⇔ 16Acyl-CoA + Car | ||
| Mechanism | Ordered Bi Bi30 | ||
| Rate equation | Eqn. 8 | ||
| Species, organ | Rat liver mitochondira | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmS1 | 6.3 x 10-4 | Class 2 | |
| KmS2 | 3.3 x 10-4 | Class 2 | |
| KmP1 | 950x10-6 | Class 0 | |
| KmP2 | 34 x 10-6 | Class 0 | |
| KiS1 | 2.4 x 10-4 | Class 2 | |
| KiS2 | 2.7 x 10-4 | Class 2 | |
| KiP1 | 41 x 10-6 | Class 0 | |
| KiP2 | 7x 10-6 | Class 0 | |
| Keq | 23540 | Class 3 | |
| KcF | 8.0 | Class 2 | |
| KcR | 2.4 | Class 0 | 1.8 Unit/mg × 80kDa, refs. 30,44 |
| Source for parameter estimation: Figure 1 with 0 μM SDZ in reference 30. | |||
Supporting Table 18.The kinetic properties of CS
| Reaction | OXA + Acetyl-CoA ⇔ Cit + CoA | ||
| Mechanism | Random Bi Bi31,34,45 | ||
| Rate equation | |||
| Species, organ | Rat kidney, rat brain | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| k1 | 6.8 × 1010 | Class 3 | |
| k _1 | 8.1 × 10 8 | Class 3 | |
| k2 | 3.0 × 1010 | Class 3 | |
| k_2 | 7.2 × 10 8 | Class 3 | |
| k3 | 6.2 × 1010 | Class 3 | |
| k_3 | 5.1 × 108 | Class 3 | |
| k4 | 1.2 × 1010 | Class 3 | |
| k_4 | 4.0 × 108 | Class 3 | |
| k5 | 1.4 × 109 | Class 3 | |
| k_5 | 2.4 × 108 | Class 3 | |
| k6 | 4.1 × 1010 | Class 3 | |
| k_6 | 1.1 × 10 8 | Class 3 | |
| k7 | 5 × 1010 | Class 3 | |
| k_7 | 9.8 × 108 | Class 3 | |
| k8 | 5.3 × 1010 | Class 3 | |
| k_8 | 7.7 × 10 8 | Class 3 | |
| Source for parameter estimation: reference 31. | |||
Supporting Table 19.The kinetic properties of DIC
| Reaction | Mal(IMS) + Pi(MAT) ⇔ Mal(MAT) + Pi(IMS) | ||
| Mechanism | Rapid equilibrium random Bi Bi46 | ||
| Rate equation | Eqn. 12 | ||
| Species, organ | Rat liver mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KiS1 | 0.20 x10-3 | Class 0 | Ref. 46, Fig.5 |
| KiS2 | 0.72 x10-3 | Class 0 | Ref. 46, Fig.5 |
| KiP1 | 9.0 x 10-4 | Class 2 | |
| KiP2 | 7.6 x 10-4 | Class 2 | |
| KcF | 2.7 | Class 0 | 6.7 × 10-6mol/min/mg × 28 kDa |
| KcR | 4.1 | Class 1 | |
| Alpha | 1.0 | Class 0 | |
| Beta | 1.0 | Class 0 | |
| Gamma | 1.0 | Class 0 | |
| Delta | 1.0 | Class 0 | |
Source for parameter estimation: Figure 5A with 0.05 mM phosphate, (C) with 0.10 mM malate in reference 46.
Supporting Table 20.The kinetic properties of ECH
| Reaction | Enoyl-CoA + H2O ⇔ 3-hydroxyacyl-CoA | ||
| Mechanism | Uni uni reversible39 | ||
| Rate equation | Eqn. 14 | ||
| Species, organ | Bovine liver | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| Ks | 16.9 × 10-6 | Class 0 | |
| Kp | 12.1 × 10-6 | Class 0 | |
| KcF | 8.9166667 | Class 0 | |
| KcR | 2154.1667 | Class 0 | |
Supporting Table 21.The kinetic properties of ETF-QO
| Reaction | ETFred + Q ⇔ ETFox + QH2 | ||
| Mechanism | Ping-pong Bi Bi14 | ||
| Rate equation | Eqn. 11 | ||
| Species, organ | Pig liver mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmS1 | 0.31 x 10-6 | Class 0 | |
| KmS2 | 0.39 x 10-6 | Class 2 | |
| KmP1 | 0.32 x 10-6 | Class 0 | |
| KmP2 | 4.2 x10-9 | class 2 | |
| KiS1 | 0.31 x 10-6 | Class 0 | |
| KiP2 | 0.3 x 10-6-6 | Class 2 | |
| Keq | 0.66 | Class 0 | |
| KcF | 78 | Class 0 | |
| KcR | 101 | Class 2 | |
Source for parameter estimation: Figure 4 with 1.5 μM ETF hydroquinone in reference 14.
Supporting Table 22.The kinetic properties of FM
| Reaction | Fum ⇔ Mal | ||
| Mechanism | Uni uni reversible | ||
| Rate equation | Eqn. 14 | ||
| Species, organ | |||
| Parameter | Class | Notice | |
|---|---|---|---|
| Ks | 0.5 x 10-5 | Class 0 | Ref. 47, Table V |
| Kp | 2.5 x 10-5 | Class 0 | |
| KcF | 800 | Class 0 | |
| KcR | 900 | Class 0 | |
Supporting Table 23.The kinetic properties of HCD
| Reaction | 3-hydroxyacyl-CoA + NAD+⇔ 3-oxoacyl-CoA + NADH | ||
| Mechanism | Michaelis-menten39 | ||
| Rate equation | Eqn. 6 | ||
| Species, organ | Pig heart | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| Ks | 1.5 × 10-6 | Class 0 | |
| KcF | 41.483333 | Class 0 | |
Supporting Table 24.The kinetic properties of IDHa
| Reaction | IsoCit + NAD+⇔ OG + NADH | ||
| Mechanism | Ref. 35 | ||
| Rate equation | Eqn. 5 | ||
| Species, organ | Bovine heart | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KcF | 105 | Class 0 | 28 U/mg × 224000 Da (refs. 35,48) |
| b | 29.6 | Class 3 | |
| c | 0.00023 | Class 3 | |
| d | 7.8 × 10-5 | Class 3 | |
| E | 0.00064 | Class 3 | |
| F | 0.00036 | Class 3 | |
Source for parameter estimation: Figure 4 with 1.0 mM ADP in reference 35.
Supporting Table 25.The kinetic properties of IDHb
| Reaction | IsoCit + NADP+⇔ OG + NADPH | ||
| Mechanism | See ref. 49 | ||
| Rate equation | Eqn. 5 | ||
| Species, organ | Bovine heart mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| Phi0 | 5.1 x 10-2 | Class 0 | Ref. 49, Table 1 |
| Phi1 | 9.5 x10-8 | Class 0 | |
| Phi2 | 0.96 x10-6 | Class 0 | |
| Phi12 | 9 x 10-8 | Class 0 | |
| Phir0 | 6.6 x 10-2 | Class 0 | |
| Phir1 | 0.37 x10-6 | Class 0 | |
| Phir2 | 29 x10-6 | Class 0 | |
| Phir3 | 2.5 x10-4 | Class 0 | |
| Phir12 | 6 × 10-12 | Class 0 | |
| Phir13 | 1.3 × 10 -10 | Class 0 | |
| Phir23 | 9.4 x 10-8 | Class 0 | |
| Phir123 | 4.6 × 10-14 | Class 0 | |
Supporting Table 26.The kinetic properties of MDH
| Reaction | Mal + NAD+⇔ OXA + NADH | ||
| Mechanism | Ordered Bi Bi ref. 15 | ||
| Rate equation | Eqn. 9 | ||
| Species, organ | Human liver cytosol | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmS1 | 72 x 10-6 | Class 0 | |
| KmS2 | 110 x 10-6 | Class 0 | |
| KmP1 | 1600 × 10-6 | Class 0 | |
| KmP2 | 170 x 10-6 | Class 0 | |
| KiS1 | 11 x 10-6 | Class 0 | |
| KiS2 | 100x 10-6 | Class 0 | |
| KiP1 | 7100 x 10-6 | Class 0 | |
| KiP2 | 1900 × 10-6 | Class 0 | |
| KcF | 0.390 | Class 0 | Specifc activity = 0.33 U/mg, |
| MW = 72000 (ref. 15, Table I) | |||
| KcR | 0.040 | Class 0 | Vf/Vr = 9.8 (ref. 15, Table III) |
Supporting Table 27.The kinetic properties of NDK
| Reaction | ATP + GDP ⇔ ADP + GTP | ||
| Mechanism | Ping-pong Bi Bi50,51 | ||
| Rate equation | Eqn. 11 | ||
| Species, organ | Yeast | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmS1 | 0.31 x 10-3 | Class 0 | Ref. 51 |
| KmS2 | 0.043 x 10-3 | Class 0 | Ref. 51, UDP |
| KmP1 | 0.050 x 10-3 | Class 0 | Ref. 51 |
| KmP2 | 0.25 x 10-3 | Class 0 | Ref. 51, UTP |
| KiS1 | 0.21 x 10-3 | Class 2 | Ref. 51 |
| KiP2 | 0.35 x 10-3 | Class 2 | Ref. 51, UTP |
| Keq | 1.28 | Class 0 | Ref. 51 |
| KcF | 6883 | Class 0 | MW = 70000 Da, ref. 50 |
| KcR | 5950 | Class 0 | MW = 70000 Da, ref. 50 |
Source for parameter estimation: Figure 4 with 0.18 mM ATP in reference 50.
Supporting Table 28.The kinetic properties of OCT
| Reaction | 3-oxoacyl-CoA + CoA ⇔ Acyl-CoA + Acetyl-CoA | ||
| Mechanism | Ping-pong Bi Bi33 | ||
| Rate equation | Eqn. 11 | ||
| Species, organ | Rat liver mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmS1 | 1.1 x 10-6 | Class 0 | OCTa |
| 1.10 x 10-6 | Class 0 | OCTb, value for 16Oxoacyl-CoA | |
| 1.30 × 10-6 | Class 0 | OCTc | |
| 2.10x10-6 | Class 0 | OCTd | |
| 3.20x10-6 | Class 0 | OCTe | |
| 6.70x10-6 | Class 0 | OCTf | |
| 1.24 × 10-6 | Class 0 | OCTg | |
| KmS2 | 28.6 x10-6 | Class 0 | |
| 2.86 x10-6 | Class 0 | OCTb, value for 16Oxoacyl-CoA | |
| 3.84 x10-6 | Class 0 | OCTc | |
| 3.57x10-6 | Class 0 | OCTd | |
| 3.55 x10-6 | Class 0 | OCTe | |
| 1.89 × 10-6 | Class 0 | OCTf | |
| 2.20x10-6 | Class 0 | OCTg | |
| KmP1 | 7.2 × 10-5 | Class 2 | |
| KmP2 | 8.7x10-5 | Class 2 | |
| KiS1 | 1.1 x 10-5 | Class 2 | |
| KiP2 | 8.7x10-5 | Class 2 | |
| Keq | 160.98 | Class 3 | |
| KcF | 137.86 | Class 0 | Vma × 178000 Da |
| 137.86 | Class 0 | OCTb, value for 16Oxoacyl-CoA | |
| 253.52 | Class 0 | OCTc | |
| 272.94 | Class 0 | OCTd | |
| 277.38 | Class 0 | OCTe | |
| 264.07 | Class 0 | OCTf | |
| 80.244 | Class 0 | OCTg | |
| KcR | 87.253 | Class 2 | |
| 87.253 | Class 2 | OCTb, value for 16Oxoacyl-CoA | |
| 160.46 | Class 2 | OCTc | |
| 172.75 | Class 2 | OCTd | |
| 175.56 | Class 2 | OCTe | |
| 167.13 | Class 2 | OCTf | |
| 51.615 | Class 2 | OCTg | |
Source for parameter estimation: Figure 5B with 200 μM Acetyl-CoA in reference 33.
Supporting Table 29.The kinetic properties of OGC
| Reaction | OG(IMS) + Mal(MAT) ⇔ OG(MAT) + Mal(IMS) | ||
| Mechanism | Rapid equilibrium random Bi Bi23 | ||
| Rate equation | Eqn. 12 | ||
| Species, organ | Bovine heart mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KiS1 | 0.3 x 10-3 | Class 0 | |
| KiS2 | 0.7 x 10-3 | Class 2 | |
| KiP1 | 1.4 x 10-3 | Class 0 | |
| KiP2 | 0.17 x 10-3 | Class 2 | |
| KcF | 3.675 | Class 0 | |
| KcR | 4.83 | Class 0 | |
| Alpha | 1.0 | Class 0 | |
| Beta | 1.0 | Class 0 | |
| Gamma | 1.0 | Class 0 | |
| Delta | 1.0 | Class 0 | |
Source for parameter estimation: Figure 2 with 20 mM malate in reference 23.
Supporting Table 30.The kinetic properties of OGDC
| Reaction | OG + NAD++ CoA → SCoA + NADH + CO2 | ||
| Mechanism | Multisite ping-pong22,52 | ||
| Rate equation | Eqn. 7 | ||
| Species, organ | Pig heart mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmA | 0.22 x 10-3 | Class 0 | Pig heart ref. 22 |
| KmB | 0.025 x 10-3 | Class 0 | Pig heart ref. 22 |
| KmC | 0.050 x 10-3 | Class 0 | Pig heart ref. 22 |
| KmP | 3 x 10-4 | Class 2 | |
| KmR | 6 x 10-4 | Class 2 | |
| K ia | 7.2 x 10-4 | Class 2 | 0.75 x 10-3, Dictyostelium, |
| K ib | 7.4 x 10-4 | Class 2 | |
| Kic | 1 x 10-4 | Class 2 | |
| Kip | 1.1 x 10-6 | Class 2 | |
| Kiq | 81 x 10-6 | Class 0 | Human heart ref. 53 |
| Kir | 25 x 10-6 | Class 0 | Human heart ref. 53 |
| KcF | 177 | Class 2 | Estimated, 270 at MW = 2700000 Da |
Source for parameter estimation: Figure 1A with 0.010 mM CoA, (B) with 0.20 mM NAD+, (C) with 0.10mM oxoglutarate in reference 22.
Supporting Table 31.The kinetic properties of PC
| Reaction | Pyr + ATP + CO2⇔ OXA + ADP + Pi | ||
| Mechanism | Ref. 13 | ||
| Rate equation | Eqn. 10 | ||
| Species, organ | Chicken liver | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmA | 0.11 × 10-3 | Class 0 | ATP, Table III, inhibitor = MgADP |
| KmB | 1.63 x 10-3 | Class 0 | HCO3, Table III, inhibitor = OXA |
| KmC | 0.37 x 10-3 | Class 0 | Pyr, Table III, inhibitor = OXA |
| KmP | 16 x 10-3 | Class 0 | Pi, Table III, inhibitor = MgATP |
| KmQ | 0.24 x 10-3 | Class 0 | ADP, Table III, inhibitor = MgATP |
| KmR | 0.051 x 10-3 | Class 0 | OXA, Table III, inhibitor = Pyr |
| Keq | 9.0 | Class 0 | |
| Kia | 0.15 × 10-3 | Class 0 | ATP, Table I |
| Kib | 1.6 × 10-3 | Class 0 | HCO3 , Table I |
| Kic | 0.13 × 10-3 | Class 0 | Pyr, Table III, vs OXA |
| Kip | 7.9 × 10-3 | Class 0 | Pi, Table I |
| Kiq | 0.19 × 10-3 | Class 0 | ADP, Table I |
| Kir | 0.24 x 10-3 | Class 0 | OXA, Table III, vs Pyr |
| KcF | 200 | Class 0 | Specifc activity = 20, MW = 600000 |
| KcR | 20 | Class 0 | V1/V2 = 10 |
Supporting Table 32.The kinetic properties of PDC
| Reaction | Pyr + NAD++ CoA ⇔ Acetyl-CoA + NADH + CO2 | ||
| Mechanism | Multisite ping-pong22,52 | ||
| Rate equation | Eqn. 7 | ||
| Species, organ | Pig heart mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmA | 25 x 10-6 | Class 0 | Ref. 53 |
| KmB | 13 x 10-6 | Class 0 | Ref. 53 |
| KmC | 50 x 10-6 | Class 0 | Ref. 53 |
| KmP | 5.9 x10-7 | Class 2 | |
| KmR | 6.9 x 10-7 | Class 2 | |
| Kia | 5.5 x 10-4 | Class 2 | Dictyostelium, ref. 54 |
| Kib | 3.0 x 10-4 | Class 2 | |
| Kic | 1.8 x 10- 4 | Class 2 | |
| Kip | 6.0 x 10-5 | Class 2 | |
| Kiq | 35 x 10-6 | Class 0 | Human heart, ref. 53 |
| Kir | 36 x 10-6 | Class 0 | Human heart, ref. 53 |
| KcF | 856 | Class 1 | Specifc activity = 4.8 U/mg protein ref. 53 |
Source for parameter estimation: Figure 2A with 0.015 mM CoA, (B) with 0.050 mM NAD+, (C) with 0.050 mM pyruvate in reference 22.
Supporting Table 33.The kinetic properties of PIC
| Reaction | Pi(IMS) + H+(IMS) ⇔ Pi(MAT) + H+(MAT) | ||
| Mechanism | Rapid equilibrium random Bi Bi38 | ||
| Rate equation | Eqn. 12 | ||
| Species | Rat heart mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KiS1 | 0.87 | Class 2 | |
| KiS2 | 1.86 x 10-8 | Class 2 | |
| KiP1 | 32.84 x 10-9 | Class 0 | Fig. 4, ref. 38 |
| KiP2 | 11.12 × 10-3 | Class 0 | Fig. 4, ref. 38 |
| KcF | 37.9 | Class 0 | Fig. 4, ref. 38 |
| KcR | 37.0 | Class 0 | Fig. 4, ref. 38 |
| Alpha | 1.0 | Class 0 | |
| Beta | 1.0 | Class 0 | |
| Gamma | 1.0 | Class 0 | |
| Delta | 1.0 | Class 0 | |
Source for parameter estimation: Figure 4A with pH5.85, (B) with 4 mM phosphate in reference 38.
Supporting Table 34.The kinetic properties of PYC
| Reaction | Pyr(IMS) + H+(MAT) ⇔ Pyr(MAT) + H+(IMS) Rapid equilibrium random Bi Bi | ||
| Mechanism | (“Sequential Mechanism” in ref. 55) | ||
| Rate equation | Eqn. 12 | ||
| Species, organ | Rat liver mitochondria | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KiS1 | 6.1 × 10-4 | Class 2 | |
| KiS2 | 5.9 x 10-4 | Class 2 | |
| Kip1 | 2.6 x 10-4 | Class 2 | |
| Kip2 | 4.1 x 10-4 | Class 2 | |
| KcF | 0.84 | Class 1 | 0.67 ref. 56 |
| KcR | 0.78 | Class 0 | 0.61 ref. 56 |
| Alpha | 1.0 | Class 0 | |
| Beta | 1.0 | Class 0 | |
| Gamma | 1.0 | Class 0 | |
| Delta | 1.0 | Class 0 | |
Source for parameter estimation: Figure 3 in reference 56.
Supporting Table 35.The kinetic properties of SCS
| Reaction | SCoA + GDP + Pi ⇔ Suc + CoA + GTP | ||
| Mechanism | See ref. 57 | ||
| Rate equation | Eqn. 13 | ||
| Species, organ | Pig heart | ||
| Parameter | Class | Notice | |
|---|---|---|---|
| KmA | 5 x 10-6 | Class 0 | GDP (2-8 × 10-6) |
| KmB | 3.5 x10-5 | Class 0 | Succinyl-CoA (1-6 x 10-5) |
| KmC | 4.5 x10-4 | Class 0 | Pi (2-7 x 10-4) |
| KmP | 6 x 10-4 | Class 0 | Succinate (4-8 x 10-4) |
| KmQ | 7.5 × 10-6 | Class 0 | GTP (5-10 x 10-6) |
| KmC2 | 4.5 x10-4 | Class 0 | Pi (2-7 x 10-4) |
| KmP | 26 × 10-4 | Class 0 | Succinate (4-8 x 10-4) |
| Keq | 8.375 | Class 0 | From haldane relationships |
| Kia | 4 x 10-4 | Class 0 | GDP (Table II) |
| Kib | 2 x 10-5 | Class 0 | Succinyl-CoA, (vs CoA, Fig. 7) |
| Kic | 3 x 10-5 | Class 0 | Pi (Table II) |
| Kip | 7 x 10-2 | Class 0 | Succinate (Table II) |
| Kiq | 5 x 10-6 | Class 0 | GTP (Table II) |
| Kir | 6.7x10-6 | Class 0 | CoA, from a haldane relationship, Kq × Kir = Kiq × Kr |
| Kc1 | 100 | Where Kr (CoA) = 10 x 10-6M | |
| Kc2 | 100 | Class 0 | Kcat = Kc2 = 25 to 287.5 (20 to 230 U/mg × 75000 dalton) |
| Kia | 4 x 10-4 | Class 3 | Guess, V1/V2 = 0.20, V2’/V1’ = 30 |
Supporting Table 36.The kinetic properties of SDH
| Reaction | Suc + Q ⇔ Fum + QH2 | ||
| Mechanism | Ping-pong Bi Bi20 | ||
| Rate equation | Eqn. 11 | ||
| Species, organ | Bovine heart mitochondria | ||
| Paramenter | Class | Notice | |
|---|---|---|---|
| KmS1 | 30x10-6 | Class 0 | |
| KmS2 | 69 x 10-46 | Class 0 | 30-130 x 10-6 |
| KmP1 | 0.3 x10-6 | Class 0 | |
| KmP2 | 1.5 x10-6 | Class 0 | |
| KiS1 | 4.1 × 10-6 | Class 2 | Ki for carbo x in = 3.0 x 10-6M |
| KiP2 | 5.6 x10-6 | Class 2 | Ki for carbo x in = 3.0 x 10-6M |
| Keq | 0.037 | Class 0 | From Haldane relationship |
| KcF | 69.3 | Class 0 | MW = 104000 Da |
| KcR | 1.73 | Class 0 | MW = 104000 Da |
Source for parameter estimation: Figure 2B in reference 20.
Rate Equations
AAC

Complex III
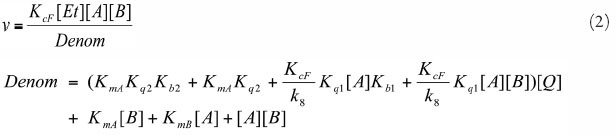
Complex V

IDHa
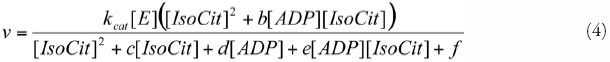
IDHb

Michaelis-Menten

Multisite Ping-Pong

Ordered Bi Bi (1)

Ordered Bi Bi (2)
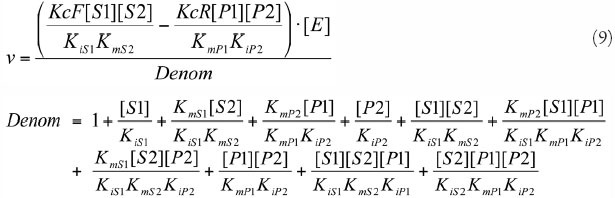
PC

Ping-Pong Bi Bi
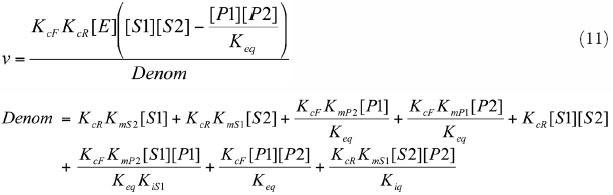
Rapid Equilibrium Random Bi Bi
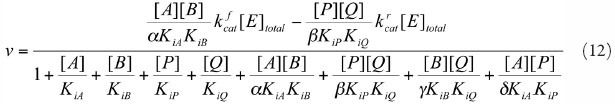
SCS

Uni Uni Reversible
- Dynamic Kinetic Modelling of Mitochondrial Energy Metabolism - Madame Curie Bios...Dynamic Kinetic Modelling of Mitochondrial Energy Metabolism - Madame Curie Bioscience Database
- Calcium Channel Block and Inactivation: Insights from Structure-Activity Studies...Calcium Channel Block and Inactivation: Insights from Structure-Activity Studies - Madame Curie Bioscience Database
- Scaling Laws in the Functional Content of Genomes: Fundamental Constants of Evol...Scaling Laws in the Functional Content of Genomes: Fundamental Constants of Evolution? - Madame Curie Bioscience Database
- PDGF Pathways and Growth of Basal Cell and Squamous Cell Carcinomas - Madame Cur...PDGF Pathways and Growth of Basal Cell and Squamous Cell Carcinomas - Madame Curie Bioscience Database
- Phylogenetic, Structural and Functional Relationships between WD-and Kelch-Repea...Phylogenetic, Structural and Functional Relationships between WD-and Kelch-Repeat Proteins - Madame Curie Bioscience Database
Your browsing activity is empty.
Activity recording is turned off.
See more...