NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.
Evidence reviews for the clinical and cost effectiveness of treatment regimens for the treatment of operable Stage IIIA-N2 NSCLC
Review questions
RQ3.1: What is the clinical and cost effectiveness of chemoradiotherapy or surgery with adjuvant treatment for the treatment for N2 stage NSCLC?
Introduction
The aim of the review is to provide clearer guidance regarding the treatment of stage IIIA-N2 NSCLC. This is because the roles of surgery and chemoradiotherapy in this setting are extensively debated.
Table 1PICO table
| Population | People with stage N2 M0 NSCLC |
|---|---|
| Interventions | Surgery (S) with or without chemotherapy (C) |
| Comparators |
|
| Outcomes |
|
Methods and process
This evidence review was developed using the methods and process described in Developing NICE guidelines: the manual (2014). Methods specific to this review question are described in the review protocol in appendix A, and the methods section in appendix B. In particular, the minimally important differences (MIDs) used in this review are summarised in appendix B.
Declarations of interest were recorded according to NICE’s 2018 conflicts of interest policy.
One thousand abstracts were screened manually.
This review includes several network meta-analysis performed by the NICE Guidelines Technical Support Unit (TSU), which is based at the University of Bristol and the University of Leicester.
Clinical evidence
Included studies
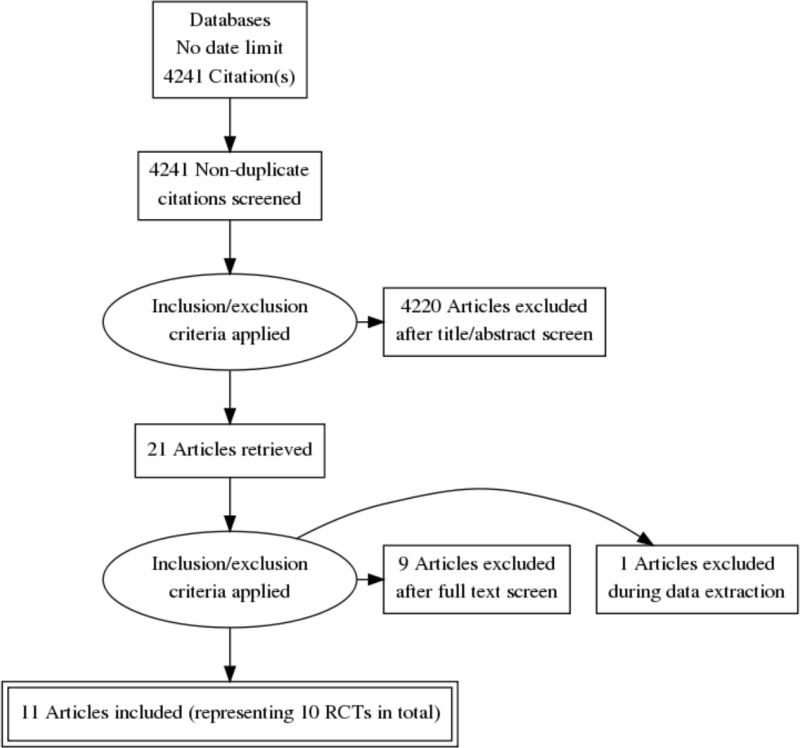
This review was conducted as part of a larger update of the NICE Lung cancer: diagnosis and management guideline (CG 121). A systematic literature search for randomised controlled trials (RCTs) with a no date limit yielded 4,241 references.
Papers returned by the literature search were screened on title and abstract, with 21 full-text papers ordered as potentially relevant systematic reviews or RCTs.
Eleven papers representing 10 unique RCTs were included after full text screening. The RCTs were: Albain 2009 (n=396, follow-up period was a minimum of 2.5 years), Eberhardt 2015 (n=161, follow-up period was a minimum of 1 year), Girard 2010 (n=46, the median follow-up period was 31.4 months), Johnstone 2002 (n=61, follow up period was a minimum of 4 years), Katakami 2012 (n=56, follow-up period was a minimum of 5 years), Pless 2015 (n=231, the median follow-up period was 52 months), Shepherd 1998 (n=31, follow-up was 24 months in one arm and 31 months in the other), Stephens 2005 (n=48, the median follow-up period was 14 months), Thomas 2008 (n=524, the median follow-up period was 70 months) and van Meerbeeck 2007 (n=208, the median follow-up period was 6 years).
For the search strategy, please see appendix C. For the clinical evidence study selection flowchart, see appendix D. For the full evidence tables and full GRADE profiles for included studies, please see appendices E and F.
Excluded studies
Details of the studies excluded at full-text review are given in appendix G along with a reason for their exclusion.
Summary of clinical studies included in the evidence review
Study locations
One randomised controlled study was from the UK (Stephens 2005), 1 was from France (Girard 2010), 2 were from Germany (Eberhardt 2015, Thomas 2008), 1 was from Switzerland, Germany and Serbia (Pless 2015), 1 was from the Netherlands (van Meerbeeck 2007), 1 was from the USA (Johnstone 2002), 1 was from Canada (Shepherd 1998), 1 was from the USA and Canada (Albain 2009) and 1 was from Japan (Katakami 2012).
Outcomes and sample sizes
The reported outcomes with extractable data were mortality and adverse events. The sample sizes ranged from 31 participants to 524 across studies.
See full evidence tables and Grade profiles in appendices E and F.
Quality assessment of clinical studies included in the evidence review
See appendix E for full GRADE tables.
Economic evidence
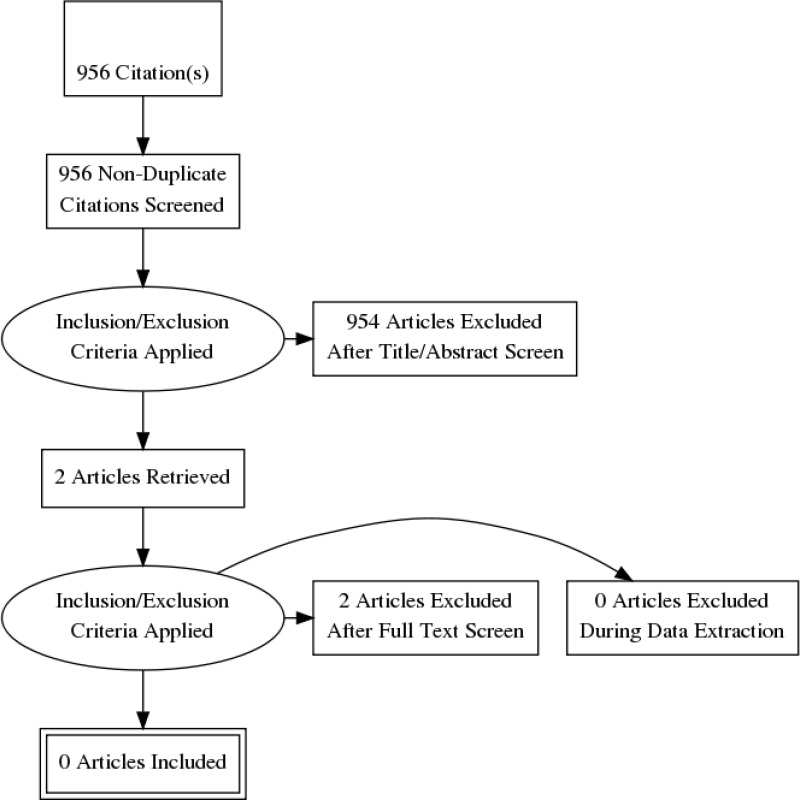
Standard health economic filters were applied to the clinical search for this question, and a total of 956 citations were returned. Following review of titles and abstracts, two full text studies were retrieved for detailed consideration, but these were subsequently excluded as not relevant. Therefore, no relevant cost–utility analyses were identified for this question.
This review question was prioritised for economic modelling, and an original economic model was developed.
Summary of original economic model
The de novo cost-utility analysis developed for this guideline included three strategies; chemoradiotherapy (CR), chemotherapy and surgery (CS) and chemoradiotherapy and surgery (CRS). It was based on a hybrid structure where the amount of time that patients spent in the progression free and progressed states, the probability of survival and the adverse events during the first five years were drawn from network meta-analyses conducted for this guideline. Survival in patients still alive after five years was modelled using patient registry data. The model included costs for the initial interventions and for treatment on progression, deaths, adverse events and routine costs associated with the progression free and progressed states. The model included utility estimates for both states as well as longer term survival and a disutility adjustment in the surgical arm. In accordance with data from the underpinning trials, not all patients in surgical strategies went on to receive surgery following chemoradiotherapy. Patients entered the model at age 60, which reflected the average age in the underpinning trials. The cycle length was one month and costs and health benefits were discounted at 3.5% per year.
The model found that CS was extendedly dominated by CR and CRS and had an ICER of £52,400/QALY versus CR. CRS was cost-effective compared to CR with an ICER of £16,900/QALY. These results were robust to a wide range of sensitivity and scenario analyses. The probabilistic sensitivity analysis showed that CRS produced more QALYs than CR and CS in 97% and 87% of iterations respectively. There were, however, key uncertainties in the underpinning clinical data with no individual pairwise studies having reported significant differences in overall survival. No subgroup analyses were performed. The full modelling report is available in Appendix K.
Evidence statements
The outcomes reported in network meta-analyses were not directly reported in the underpinning trials and therefore, although the trials are the same, there are no corresponding evidence statements for pairwise comparisons. Progression free survival time, post-progression survival time and the probability of survival were calculated using data extracted from survival graphs and ‘number at risk’ tables available in the underpinning studies.
C = chemotherapy, R = radiotherapy, S = surgery.
CRS vs CR vs CS (network meta-analysis)
Moderate quality evidence from 1 network meta-analysis that included more than 1,000 patients across 6 RCTs could not distinguish the odds of survival at 4 years between the interventions.
Moderate quality evidence from 1 network meta-analysis that included more than 1,000 patients across 5 RCTs could not distinguish the odds of survival at 5 years between the interventions.
High quality evidence from 1 network meta-analysis that included more than 1,000 patients across 6 RCTs found that CRS was associated with a longer progression-free survival time than both CS and CR at 4 years. The data could not differentiate CS from CR.
High quality evidence from 1 network meta-analysis that included more than 1,000 patients across 5 RCTs found that CRS was associated with a longer progression-free survival time than both CS and CR at 5 years. The data could not differentiate CS from CR.
High quality evidence from 1 network meta-analysis that included more than 1,000 patients across 6 RCTs could not distinguish post-progression survival time at 4 years.
High quality evidence from 1 network meta-analysis that included more than 1,000 patients across 5 RCTs could not distinguish post-progression survival time at 5 years.
Moderate quality evidence from 1 network meta-analysis that included more than 1,000 patients across 6 RCTs could not distinguish total life years at 4 years between the interventions.
Moderate quality evidence from 1 network meta-analysis that included more than 1,000 patients across 5 RCTs could not distinguish total life years at 5 years between the interventions.
High quality evidence from 1 network meta-analysis that included more than 1,000 patients across 4 RCTs found that CCRS was associated with a lower hazard ratio of adverse events at grade 3+ than both CS and CR.
CRS vs CR
Moderate-quality evidence from 1 RCT reporting data on 396 people with N2 NSCLC found that the data could not differentiate for mortality (all-cause hazard ratio). However, high to moderate-quality evidence found there were a greater number of participants who experienced anaemia, nausea and/or emesis, oesophagitis and pulmonary (adverse events grade 3 or above) in the CR group compared to the CRS group. The data could not differentiate for eukopenia, neutropenia, thrombocytopenia, worst haematologic toxicity per patient, neuropathy, stomatitis and/or mucositis, other gastrointestinal or renal, cardiac, miscellaneous infection, haemorrhage, fatigue, anorexia or allergy (adverse events grade 3 or above).
CRS vs CS
Very low to moderate-quality evidence from 3 RCTs reporting data on 333 people with NSCLC found that the data could not differentiate for mortality (all-cause hazard ratio and risk ratio for survival at 1, 2 and 3 years), stomatitis, dyspnoea and pneumonitis (adverse events grade 3 or above).
C, CRS vs C, CR boost
Moderate to high-quality evidence from 1 RCT reporting data from 161 people with potentially resectable stage IIIA (N2) or selected stage IIIB NSCLC found that the data could not differentiate for mortality at 1 year, 2 years, 3 years, 4 years, 5 years and 6 years. However, there were a greater number of participants who experienced oesophagitis in the C, CR boost group compared to the C, CRS group. The data could not differentiate for leukopenia, anaemia, thrombocytopenia, nausea/vomiting, neuropathy, mucositis/stomatitis, pulmonary, other GI or renal, cardiac, miscellaneous infection, fatigue, pain (adverse events grade 3 or above) or dropout during treatment.
CS vs CR
Very low to moderate-quality evidence from 2 RCTs reporting data from 369 people with N2 NSCLC found that the data could not differentiate for mortality at 1 year, 2 years, 3 years and 4 years. Neither could the data differentiate for treatment-related mortality nor dropout during treatment.
CS vs CRS (cisplatin + docetaxel)
Moderate to high-quality evidence from 1 RCT reporting data from 231 people who had stage IIIA (T1-3) N2 NSCLC found the CS group had a greater number of people who experienced infection compared to the CRS (cisplatin + docetaxel) group. The data could not differentiate for mortality (all-cause hazard ratio), alopecia, nausea/vomiting, fatigue, diarrhoea, neurotoxic effects, stomatitis, skin toxic effects, dyspnoea, fluid retention, constipation, febrile neutropenia, fever, allergic reaction, neutropenia, leukopenia, thrombocytopenia, anaemia (adverse events grade 3 or above), or dropout during treatment.
CS vs R
Very low to low-quality evidence from 2 RCTs reporting data from 79 people who had NSCLC T3, N1, M0 or T1-3, N2, M0 found that the data could not differentiate for mortality, lethargy (this adverse event was grade 2 or above) or dropout during treatment.
C, CRS, R vs CRS
Very low-quality evidence from 1 RCT reporting data from 524 people with NSCLC stage IIIA (T1-3, N2, M0 or central T3, N0-1, M0) or stage IIIB (T4, N1-3, M0 or T1-4, N3, M0) found that the data could not differentiate for mortality (all-cause hazard ratio or treatment related). However, there were a greater number of people who experienced haemotoxicity in the C, CRS, R group compared to the CRS group. There were a greater number of people who experienced pneumonitis in the CRS compared to the C, CRS, R group. The data could not differentiate for oesophagitis and peri-operative complications (adverse events were grade 3 or above).
Health economics evidence statements
Evidence from one directly applicable original health economic model with minor limitations built for this guideline showed that chemoradiotherapy with surgery is very likely to be more cost-effective than chemoradiotherapy (pairwise ICER = £19,800/QALY) and chemotherapy with surgery (pairwise ICER = £4,200) per QALY. The model’s conclusions were largely insensitive to changes in model parameters and assumptions.
The committee’s discussion of the evidence
Interpreting the evidence
The outcomes that matter most
The committee agreed that the outcome that matters the most is mortality. This is because the purpose of chemotherapy, radiotherapy and surgery is to reduce mortality as much as possible. Secondary outcomes were progression-free survival, severe adverse events and quality of life.
The quality of the evidence
The committee agreed that the aim of the review question was to try to establish a standard approach to managing operable NSCLC stage IIIA-N2. Ten of the 11 RCTs included in this review question could not differentiate mortality.
The committee agreed that the six trials most relevant to current practice were Pless 2015, Katakami 2012, Albain 2009, Eberhardt 2015, Girard 2010 and van Meerbeeck 2007. For the first four of these trials, outcomes were largely graded as moderate quality evidence. For the final two, outcomes were largely graded as low quality evidence. Overall survival time, progression-free survival time, probability of survival at study endpoint and adverse event data were then combined in network meta-analyses (NMA). Because the overall and progression free survival curves in the included studies did not typically exhibit proportional hazards, the committee felt it was more appropriate to use survival times and probabilities in the NMAs than hazard ratios. The fixed effects network meta-analyses found that patients receiving chemoradiotherapy and surgery spent significantly longer progression free than those receiving chemotherapy and surgery or chemoradiotherapy alone, that patients receiving chemoradiotherapy alone spent significantly longer in the post-progression state than those receiving the surgical options and that there was a strong but statistically insignificant trend favouring chemoradiotherapy and surgery over the other two interventions for overall survival time and probability of survival at study endpoint. While model fit statistics did not suggest that it fit the data any better, the random effects network meta-analyses used in sensitivity analysis found no statistically significant difference for any outcome between any of the interventions. The committee noted that only one of the RCTs found a statistically significant difference in PFS but that it was also the case that the direction of effect for this outcome in each of the studies was positive for CRS. See Appendix J for more details on the NMAs conducted for this question.
The committee were aware that PFS is a less reliable outcome than OS and discussed the potential for radiotherapy scarring to affect reliability. They did not think that there would be systematic overdiagnosis of disease progression in the nonsurgical arms of the RCTs and thereby overestimation of the PFS benefit associated with surgery. Indeed, they noted that it is possible that subtle changes in disease status are missed in patients undergoing CR because of radiotherapy scarring. They therefore felt that if bias towards incorrect recording of progression exists, it could work in either direction.
Benefits and harms
Based on the NMAs, the committee agreed that it is likely that (particularly) progression-free survival and overall survival are better for chemoradiotherapy and surgery (CRS) than the other two options if patients are well enough for it. The NMA found that CRS was associated with a 4 month (0.32 year) improvement in progression-free survival versus chemoradiotherapy (CR). The adverse event profile of the different interventions is uncertain but pairwise and network meta-analyses estimates conducted for the health economic model favoured CRS. The committee were unsure about the clinical plausibility of this, given that CRS is the most intensive intervention but agreed that there was no evidence that it was more harmful than the other two interventions. The committee agreed it was likely that there would be some quality of life loss in the months following the interventions as patients recovered. This was expected to be particularly true of the interventions including surgery.
The committee acknowledged the statistical uncertainty in outcomes reported in the individual trials but noted that the health economic model, which took into account the joint uncertainty in a number of survival outcomes, found a 89% probability that CRS would generate more life years than CR for the average patient. When the most uncertain survival outcome, the probability of survival at study endpoint (there was only an 86% probability that more people survived 5 years after treatment in the CRS arm than the CR arm) was set equal, the model found a 78% probability that CRS would generate more life years than CR.
Cost effectiveness and resource use
An original health economic model was developed to answer this question (the full modelling report is available in Appendix K). Outcomes in the first five years of this model were calculated via the network meta-analyses conducted for this guideline (Appendix I), which showed that chemoradiotherapy and surgery (CRS) was associated with a statistically significantly longer progression free survival time than chemoradiotherapy alone (CR) and that CRS showed a high probability of being associated with greater overall survival. After the first five years, it was assumed that those patients who were still alive would continue progression free until the end of the model. Their overall survival was estimated using data from an epidemiological dataset on NSCLC stage IIIA-N2 patients who had survived five years after diagnosis.
The model found that while CRS was the most expensive intervention, it was also the most cost-effective, with a base case ICER of less than £20,000/QALY gained versus CR. Chemotherapy and surgery (CS) was extendedly dominated by the combination of CRS and CR and was itself not cost-effective compared to CR with highly uncertain ICERs that were consistently above £30,000/QALY gained in sensitivity analyses.
The committee discussed the limitations of the model and the assumptions that had been needed through lack of high quality directly available data and decided that the analysis was robust for decision making purposes because its results were quite insensitive to realistic variations in uncertain data and assumptions. They noted, however, that none of the RCTs included in the NMAs found any difference in overall survival, which was the most important outcome. Taking all the above considerations together, they decided that a ‘consider’ recommendation in favour of CRS was justified by the evidence. This is because while they thought that CRS is likely to be the most cost-effective intervention and that CS was unlikely to be cost-effective compared to the other two interventions, there were a number of key uncertainties in the clinical data.
Surgery and radical radiotherapy are expensive interventions, costing approximately £7,500 and £2,500 respectively. The committee thought that only a small number of stage IIIA-N2 patients are currently treated with CRS and that these recommendations therefore represent an increase in resource use, which will depend on the extent of take-up.
Other factors the committee took into account
The committee noted that none of the trials underpinning the network meta-analysis and health economic model were conducted in a UK setting and many recruited before the widespread adoption of newer and more effective treatments for advanced NSCLC such as targeted and immunotherapies. There have also been significant innovations in surgery and radiotherapy techniques in recent years. The survival data might therefore not reflect outcomes that would be seen in UK practice today although none of these things in themselves provide reasons to reject the differential effectiveness observed in the network meta-analyses. They noted that promising evidence on the use of immunotherapy in unresectable stage III disease is available from the PACIFIC trial but concluded that that evidence was out of the scope of this question on the management of patients with stage IIIA-N2 NSCLC that is considered operable.
The committee discussed the evidence from an NMA conducted for the economic model which showed the odds ratio of death before progression was higher in the surgical interventions. They felt that this outcome was unsurprising in interventions that are more invasive in nature and noted that the other NMAs had already accounted for this. Additionally, death before progression occurred in relatively few patients in any arm of any included study. They felt that discussing the risks and benefits of any surgery with patients is common practice.
The committee agreed that tri-modality therapy requires MDTs who have expertise in all three components.
The committee noted that patient fitness and patient choice were important factors in deciding between interventions and tried to reflect this in their recommendations. The recommendations for a 3-5 week wait between CR and surgery reflect current clinical practice. This is similar to the waiting period between CR and surgery in the most relevant studies: Pless 2015, 21-28 days; Katakami 2012, 3-5 weeks; Albain 2009, 3-5 weeks; Eberhardt 2015, median of 37 days (20-61 day range); Girard 2010, 4-6 weeks.
Appendix A. Review protocols
Review protocol for the clinical and cost effectiveness of chemoradiotherapy or surgery with adjuvant treatment for the treatment for N2 stage NSCLC
| Field (based on PRISMA-P | Content |
|---|---|
| Review question | What is the clinical and cost effectiveness of chemoradiotherapy or surgery with adjuvant treatment for the treatment for N2 stage NSCLC? |
| Type of review question | Intervention |
| Objective of the review | To provide clearer guidance regarding the treatment of N2 stage NSCLC. This question was identified during scoping meeting 2. Variation in practice has also been identified. |
| Eligibility criteria – population/ disease/ condition/ issue/ domain | People with stage N2 M0 NSCLC. |
| Eligibility criteria – intervention(s)/ exposure(s)/ prognostic factor(s) | Surgery with/ without chemotherapy |
| Eligibility criteria – comparator(s)/ control or reference (gold) standard | 1. Chemoradiotherapy (radiotherapy and chemotherapy) versus 2. Tri-modality treatment |
| Outcomes and prioritisation |
|
| Eligibility criteria – study design |
|
| Other inclusion exclusion criteria |
|
| Proposed sensitivity/sub-group analysis, or metaregression | No subgroup analysis identified |
| Selection process – duplicate screening/select ion/analysis | 10% of the abstracts were reviewed by two reviewers, with any disagreements resolved by discussion or, if necessary, a third independent reviewer. If meaningful disagreements were found between the different reviewers, a further 10% of the abstracts were reviewed by two reviewers, with this process continued until agreement is achieved between the two reviewers. From this point, the remaining abstracts will be screened by a single reviewer. This review made use of the priority screening functionality with the EPPI-reviewer systematic reviewing software. See Appendix B for more details. |
| Data management (software) | See appendix B. |
| Information sources – databases and dates | No date limit. See appendix C. Main Searches:
Citation searching will be carried out in addition on analyst/committee selected papers. The search will not be date limited because this is a new review question. |
| Identify if an update | Update. Original Question (linked): What is the most effective treatment for patients with resectable non-small cell lung cancer? Recommendations that may be affected: 1.4.27 Patients with stage I or II NSCLC who are medically inoperable but suitable for radical radiotherapy should be offered the CHART regimen. [2005] |
| Author contacts | Guideline update |
| Highlight if amendment to previous protocol | For details please see section 4.5 of Developing NICE guidelines: the manual |
| Search strategy – for one database | For details please see appendix C |
| Data collection process – forms/duplicate | A standardised evidence table format will be used, and published as appendix G (clinical evidence tables) or H (economic evidence tables) of the full guideline. |
| Data items – define all variables to be collected | For details please see evidence tables in appendix G (clinical evidence tables) or H (economic evidence tables) of the full guideline. |
| Methods for assessing bias at outcome/study level | Standard study checklists were used to critically appraise individual studies. For details please see section 6.2 of Developing NICE guidelines: the manual The risk of bias across all available evidence was evaluated for each outcome using an adaptation of the ‘Grading of Recommendations Assessment, Development and Evaluation (GRADE) toolbox’ developed by the international GRADE working group http://www For further detail see Appendix B. |
| Criteria for quantitative synthesis (where suitable) | For details please see section 6.4 of Developing NICE guidelines: the manual |
| Methods for analysis – combining studies and exploring (in)consistency | For details please see the methods chapter of the full guideline. See appendix B. |
| Meta-bias assessment – publication bias, selective reporting bias | For details please see section 6.2 of Developing NICE guidelines: the manual. See appendix B. |
| Assessment of confidence in cumulative evidence | For details please see sections 6.4 and 9.1 of Developing NICE guidelines: the manual See appendix B. |
| Rationale/context – Current management | For details please see the introduction to the evidence review in the full guideline. |
| Describe contributions of authors and guarantor | A multidisciplinary committee developed the guideline. The committee was convened by NICE Guideline Updates Team and chaired by Gary McVeigh in line with section 3 of Developing NICE guidelines: the manual. Staff from NICE Guideline Updates Team undertook systematic literature searches, appraised the evidence, conducted meta-analysis and cost-effectiveness analysis where appropriate, and drafted the guideline in collaboration with the committee. For details please see the methods chapter of the full guideline. |
| Sources of funding/support | The NICE Guideline Updates Team is an internal team within NICE. |
| Name of sponsor | The NICE Guideline Updates Team is an internal team within NICE. |
| Roles of sponsor | The NICE Guideline Updates Team is an internal team within NICE. |
| PROSPERO registration number | N/A |
Appendix B. Methods
1.1. Priority screening
The reviews undertaken for this guideline all made use of the priority screening functionality with the EPPI-reviewer systematic reviewing software. This uses a machine learning algorithm (specifically, an SGD classifier) to take information on features (1, 2 and 3 word blocks) in the titles and abstract of papers marked as being ‘includes’ or ‘excludes’ during the title and abstract screening process, and re-orders the remaining records from most likely to least likely to be an include, based on that algorithm. This re-ordering of the remaining records occurs every time 25 additional records have been screened.
Research is currently ongoing as to what are the appropriate thresholds where reviewing of abstract can be stopped, assuming a defined threshold for the proportion of relevant papers it is acceptable to miss on primary screening. As a conservative approach until that research has been completed, the following rules were adopted during the production of this guideline:
- In every review, at least 50% of the identified abstract (or 1,000 records, if that is a greater number) were always screened.
- After this point, screening was only terminated when the threshold was reached for a number of abstracts being screened without a single new include being identified. This threshold was set according to the expected proportion of includes in the review (with reviews with a lower proportion of includes needing a higher number of papers without an identified study to justify termination), and was always a minimum of 250.
- A random 10% sample of the studies remaining in the database when the threshold were additionally screened, to check if a substantial number of relevant studies were not being correctly classified by the algorithm, with the full database being screened if concerns were identified.
As an additional check to ensure this approach did not miss relevant studies, the included studies lists of included systematic reviews were searched to identify any papers not identified through the primary search.
1.2. Incorporating published systematic reviews
For all review questions where a literature search was undertaken looking for a particular study design, systematic reviews containing studies of that design were also included. All included studies from those systematic reviews were screened to identify any additional relevant primary studies not found as part of the initial search.
1.2.1. Quality assessment
Individual systematic reviews were quality assessed using the ROBIS tool, with each classified into one of the following three groups:
- High quality – It is unlikely that additional relevant and important data would be identified from primary studies compared to that reported in the review, and unlikely that any relevant and important studies have been missed by the review.
- Moderate quality – It is possible that additional relevant and important data would be identified from primary studies compared to that reported in the review, but unlikely that any relevant and important studies have been missed by the review.
- Low quality – It is possible that relevant and important studies have been missed by the review.
Each individual systematic review was also classified into one of three groups for its applicability as a source of data, based on how closely the review matches the specified review protocol in the guideline. Studies were rated as follows:
- Fully applicable – The identified review fully covers the review protocol in the guideline.
- Partially applicable – The identified review fully covers a discrete subsection of the review protocol in the guideline (for example, some of the factors in the protocol only).
- Not applicable – The identified review, despite including studies relevant to the review question, does not fully cover any discrete subsection of the review protocol in the guideline.
1.2.2. Using systematic reviews as a source of data
If systematic reviews were identified as being sufficiently applicable and high quality, and were identified sufficiently early in the review process (for example, from the surveillance review or early in the database search), they were used as the primary source of data, rather than extracting information from primary studies. The extent to which this was done depended on the quality and applicability of the review, as defined in Table 2. When systematic reviews were used as a source of primary data, and unpublished or additional data included in the review which is not in the primary studies was also included. Data from these systematic reviews was then quality assessed and presented in GRADE/CERQual tables as described below, in the same way as if data had been extracted from primary studies. In questions where data was extracted from both systematic reviews and primary studies, these were cross-referenced to ensure none of the data had been double counted through this process.
Table 2. Criteria for using systematic reviews as a source of data
1.3. Evidence synthesis and meta-analyses
Where possible, meta-analyses were conducted to combine the results of quantitative studies for each outcome. For continuous outcomes analysed as mean differences, where change from baseline data were reported in the trials and were accompanied by a measure of spread (for example standard deviation), these were extracted and used in the meta-analysis. Where measures of spread for change from baseline values were not reported, the corresponding values at study end were used and were combined with change from baseline values to produce summary estimates of effect. These studies were assessed to ensure that baseline values were balanced across the treatment groups; if there were significant differences at baseline these studies were not included in any meta-analysis and were reported separately. For continuous outcomes analysed as standardised mean differences, where only baseline and final time point values were available, change from baseline standard deviations were estimated, assuming a correlation coefficient of 0.5.
1.4. Evidence of effectiveness of interventions
1.4.1. Quality assessment
Individual RCTs and quasi-randomised controlled trials were quality assessed using the Cochrane Risk of Bias Tool. Other study were quality assessed using the ROBINS-I tool. Each individual study was classified into one of the following three groups:
- Low risk of bias – The true effect size for the study is likely to be close to the estimated effect size.
- Moderate risk of bias – There is a possibility the true effect size for the study is substantially different to the estimated effect size.
- High risk of bias – It is likely the true effect size for the study is substantially different to the estimated effect size.
Each individual study was also classified into one of three groups for directness, based on if there were concerns about the population, intervention, comparator and/or outcomes in the study and how directly these variables could address the specified review question. Studies were rated as follows:
- Direct – No important deviations from the protocol in population, intervention, comparator and/or outcomes.
- Partially indirect – Important deviations from the protocol in one of the population, intervention, comparator and/or outcomes.
- Indirect – Important deviations from the protocol in at least two of the following areas: population, intervention, comparator and/or outcomes.
1.4.2. Methods for combining intervention evidence
Meta-analyses of interventional data were conducted with reference to the Cochrane Handbook for Systematic Reviews of Interventions (Higgins et al. 2011).
Where different studies presented continuous data measuring the same outcome but using different numerical scales (e.g. a 0-10 and a 0-100 visual analogue scale), these outcomes were all converted to the same scale before meta-analysis was conducted on the mean differences. Where outcomes measured the same underlying construct but used different instruments/metrics, data were analysed using standardised mean differences (Hedges’ g).
A pooled relative risk was calculated for dichotomous outcomes (using the Mantel–Haenszel method) reporting numbers of people having an event, and a pooled incidence rate ratio was calculated for dichotomous outcomes reporting total numbers of events. Both relative and absolute risks were presented, with absolute risks calculated by applying the relative risk to the pooled risk in the comparator arm of the meta-analysis (all pooled trials).
Fixed- and random-effects models (der Simonian and Laird) were fitted for all syntheses, with the presented analysis dependent on the degree of heterogeneity in the assembled evidence. Fixed-effects models were the preferred choice to report, but in situations where the assumption of a shared mean for fixed-effects model were clearly not met, even after appropriate pre-specified subgroup analyses were conducted, random-effects results are presented. Fixed-effects models were deemed to be inappropriate if one or both of the following conditions was met:
- Significant between study heterogeneity in methodology, population, intervention or comparator was identified by the reviewer in advance of data analysis. This decision was made and recorded before any data analysis was undertaken.
- The presence of significant statistical heterogeneity in the meta-analysis, defined as I2≥50%.
In any meta-analyses where some (but not all) of the data came from studies at high risk of bias, a sensitivity analysis was conducted, excluding those studies from the analysis. Results from both the full and restricted meta-analyses are reported. Similarly, in any meta-analyses where some (but not all) of the data came from indirect studies, a sensitivity analysis was conducted, excluding those studies from the analysis.
Meta-analyses were performed in Cochrane Review Manager V5.3, with the exception of incidence rate ratio analyses which were carried out in R version 3.3.4.
1.4.3. Minimal clinically important differences (MIDs)
The Core Outcome Measures in Effectiveness Trials (COMET) database was searched to identify published minimal clinically important difference thresholds relevant to this guideline. However, no relevant MIDs were found. In addition, the Guideline Committee were asked to specify any outcomes where they felt a consensus MID could be defined from their experience. In particular, any questions looking to evaluate non-inferiority (that one intervention is not meaningfully worse than another) required an MID to be defined to act as a non-inferiority margin. However, the committee agreed that in their experience, they could not define any MIDs. This is because the committee were not aware of evidence supporting the use of MIDs for the protocol’s outcomes. Therefore, the line of no effect was used as the MID for risk ratios, hazard ratios and mean differences.
1.4.4. GRADE for pairwise meta-analyses of interventional evidence
GRADE was used to assess the quality of evidence for the selected outcomes as specified in ‘Developing NICE guidelines: the manual (2014)’. Data from all study designs was initially rated as high quality and the quality of the evidence for each outcome was downgraded or not from this initial point, based on the criteria given in Table 3.Error! Reference source not found.
Table 3. Rationale for downgrading quality of evidence for intervention studies
The quality of evidence for each outcome was upgraded if any of the following three conditions were met:
- Data from non-randomised studies showing an effect size sufficiently large that it cannot be explained by confounding alone.
- Data showing a dose-response gradient.
- Data where all plausible residual confounding is likely to increase our confidence in the effect estimate.
1.4.5. Publication bias
Publication bias was assessed in two ways. First, if evidence of conducted but unpublished studies was identified during the review (e.g. conference abstracts, trial protocols or trial records without accompanying published data), available information on these unpublished studies was reported as part of the review. Secondly, where 10 or more studies were included as part of a single meta-analysis, a funnel plot was produced to graphically assess the potential for publication bias.
1.4.6. Evidence statements
Evidence statements for pairwise intervention data are classified in to one of four categories:
- Situations where the data are only consistent, at a 95% confidence level, with an effect in one direction (i.e. one that is ‘statistically significant’), and the magnitude of that effect is most likely to meet or exceed the MID (i.e. the point estimate is not in the zone of equivalence). In such cases, we state that the evidence showed that there is an effect.
- Situations where the data are only consistent, at a 95% confidence level, with an effect in one direction (i.e. one that is ‘statistically significant’), but the magnitude of that effect is most likely to be less than the MID (i.e. the point estimate is in the zone of equivalence). In such cases, we state that the evidence could not demonstrate a meaningful difference.
- Situations where the confidence limits are smaller than the MIDs in both directions. In such cases, we state that the evidence demonstrates that there is no meaningful difference.
- In all other cases, we state that the evidence could not differentiate between the comparators.
For outcomes without a defined MID or where the MID is set as the line of no effect (for example, in the case of mortality), evidence statements are divided into 2 groups as follows:
- We state that the evidence showed that there is an effect if the 95% CI does not cross the line of no effect.
- The evidence could not differentiate between comparators if the 95% CI crosses the line of no effect.
1.5. Methods for combining direct and indirect evidence (network meta-analysis) for interventions
Conventional ‘pairwise’ meta-analysis involves the statistical combination of direct evidence about pairs of interventions that originate from two or more separate studies (for example, where there are two or more studies comparing A vs B).
In situations where there are more than two interventions, pairwise meta-analysis of the direct evidence alone is of limited use. This is because multiple pairwise comparisons need to be performed to analyse each pair of interventions in the evidence, and these results can be difficult to interpret. Furthermore, direct evidence about interventions of interest may not be available. For example studies may compare A vs B and B vs C, but there may be no direct evidence comparing A vs C. Network meta-analysis overcomes these problems by combining all evidence into a single, internally consistent model, synthesising data from direct and indirect comparisons, and providing estimates of relative effectiveness for all comparators and the ranking of different interventions. Network meta-analyses were undertaken in all situations where the following three criteria were met:
- At least three treatment alternatives.
- A sufficiently connected network to enable valid estimates to be made.
- The aim of the review was to produce recommendations on the most effective option, rather than simply an unordered list of treatment alternatives.
1.5.1. Synthesis
For more information on the network meta-analysis methods and results for this review question please see appendix J.
1.5.2. Modified GRADE for network meta-analyses
A modified version of the standard GRADE approach for pairwise interventions was used to assess the quality of evidence across the network meta-analyses undertaken. While most criteria for pairwise meta-analyses still apply, it is important to adapt some of the criteria to take into consideration additional factors, such as how each ‘link’ or pairwise comparison within the network applies to the others. As a result, the following was used when modifying the GRADE framework to a network meta-analysis. It is designed to provide a single overall quality rating for an NMA, which can then be combined with pairwise quality ratings for individual comparisons (if appropriate), to judge the overall strength of evidence for each comparison.
Table 4. Rationale for downgrading quality of evidence for intervention studies
1.5.3. Quality assessment
Individual cohort and case-control studies were quality assessed using the CASP cohort study and case-control checklists, respectively. Each individual study was classified into one of the following three groups:
- Low risk of bias – The true effect size for the study is likely to be close to the estimated effect size.
- Moderate risk of bias – There is a possibility the true effect size for the study is substantially different to the estimated effect size.
- High risk of bias – It is likely the true effect size for the study is substantially different to the estimated effect size.
Individual cross-sectional studies were quality assessed using the Joanna Briggs Institute critical appraisal checklist for analytical cross sectional studies (2016), which contains 8 questions covering: inclusion criteria, description of the sample, measures of exposure, measures of outcomes, confounding factors, and statistical analysis. Each individual study was classified into one of the following groups:
- Low risk of bias – Evidence of non-serious bias in zero or one domain.
- Moderate risk of bias – Evidence of non-serious bias in two domains only, or serious bias in one domain only.
- High risk of bias – Evidence of bias in at least three domains, or of serious bias in at least two domains.
Each individual study was also classified into one of three groups for directness, based on if there were concerns about the population, predictors and/or outcomes in the study and how directly these variables could address the specified review question. Studies were rated as follows:
- Direct – No important deviations from the protocol in population, predictors and/or outcomes.
- Partially indirect – Important deviations from the protocol in one of the population, predictors and/or outcomes.
- Indirect – Important deviations from the protocol in at least two of the population, predictors and/or outcomes.
1.5.4. Methods for combining association studies
Where appropriate, hazard ratios were pooled using the inverse-variance method, and odds ratios were pooled using the Mantel-Haenszel method. Adjusted odds ratios from multivariate models were only pooled if the same set of predictor variables were used across multiple studies and if the same thresholds to measure predictors were used across studies.
Fixed- and random-effects models (der Simonian and Laird) were fitted for all syntheses, with the presented analysis dependent on the degree of heterogeneity in the assembled evidence. Fixed-effects models were the preferred choice to report, but in situations where the assumption of a shared mean for fixed-effects model were clearly not met, even after appropriate pre-specified subgroup analyses were conducted, random-effects results are presented. Fixed-effects models were deemed to be inappropriate if one or both of the following conditions was met:
- Significant between study heterogeneity in methodology, population, intervention or comparator was identified by the reviewer in advance of data analysis. This decision would need to be made and recorded before any data analysis is undertaken.
- The presence of significant statistical heterogeneity, defined as I2≥50%.
In any meta-analyses where some (but not all) of the data came from studies at high risk of bias, a sensitivity analysis was conducted, excluding those studies from the analysis. Results from both the full and restricted meta-analyses are reported. Similarly, in any meta-analyses where some (but not all) of the data came from indirect studies, a sensitivity analysis was conducted, excluding those studies from the analysis.
Meta-analyses were performed in Cochrane Review Manager v 5.3.
1.5.5. Minimal clinically important differences (MIDs)
The Core Outcome Measures in Effectiveness Trials (COMET) database was searched to identify published minimal clinically important difference thresholds relevant to this guideline. Identified MIDs were assessed to ensure they had been developed and validated in a methodologically rigorous way, and were applicable to the populations, interventions and outcomes specified in this guideline. In addition, the Guideline Committee were asked to prospectively specify any outcomes where they felt a consensus MID could be defined from their experience. In particular, any questions looking to evaluate non-inferiority (that one treatment is not meaningfully worse than another) required an MID to be defined to act as a non-inferiority margin.
MIDs found through this process and used to assess imprecision in the guideline are given in Table 5.
When decisions were made in situations where MIDs were not available, the ‘Evidence to Recommendations’ section of that review should make explicit the committee’s view of the expected clinical importance and relevance of the findings.
1.5.6. Modified GRADE for association studies
GRADE has not been developed for use with predictive studies; therefore a modified approach was applied using the GRADE framework. Data from cohort studies was initially rated as high quality, and data from case-control studies as low quality, with the quality of the evidence for each outcome then downgraded or not from this initial point.
Table 6. Rationale for downgrading quality of evidence for association studies
The quality of evidence for each outcome was upgraded if either of the following conditions were met:
- Data showing an effect size sufficiently large that it cannot be explained by confounding alone.
- Data where all plausible residual confounding is likely to increase our confidence in the effect estimate.
1.5.7. Publication bias
Publication bias was assessed in two ways. First, if evidence of conducted but unpublished studies was identified during the review (e.g. conference abstracts or protocols without accompanying published data), available information on these unpublished studies was reported as part of the review. Secondly, where 10 or more studies were included as part of a single meta-analysis, a funnel plot was produced to graphically assess the potential for publication bias.
1.6. Health economics
Literature reviews seeking to identify published cost–utility analyses of relevance to the issues under consideration were conducted for all questions. In each case, the search undertaken for the clinical review was modified, retaining population and intervention descriptors, but removing any study-design filter and adding a filter designed to identify relevant health economic analyses. In assessing studies for inclusion, population, intervention and comparator, criteria were always identical to those used in the parallel clinical search; only cost–utility analyses were included. Economic evidence profiles, including critical appraisal according to the Guidelines manual, were completed for included studies.
Economic studies identified through a systematic search of the literature are appraised using a methodology checklist designed for economic evaluations (NICE guidelines manual; 2014). This checklist is not intended to judge the quality of a study per se, but to determine whether an existing economic evaluation is useful to inform the decision-making of the committee for a specific topic within the guideline.
There are 2 parts of the appraisal process. The first step is to assess applicability (that is, the relevance of the study to the specific guideline topic and the NICE reference case); evaluations are categorised according to the criteria in Table 7.
Table 7. Applicability criteria
In the second step, only those studies deemed directly or partially applicable are further assessed for limitations (that is, methodological quality); see categorisation criteria in Table 8.
Table 8. Methodological criteria
Where relevant, a summary of the main findings from the systematic search, review and appraisal of economic evidence is presented in an economic evidence profile alongside the clinical evidence.
Appendix C. Literature search strategies
Scoping search strategies
Scoping searches Scoping searches were undertaken on the following websites and databases (listed in alphabetical order) in April 2017 to provide information for scope development and project planning. Browsing or simple search strategies were employed.
| Guidelines/website |
|---|
| American Cancer Society |
| American College of Chest Physicians |
| American Society for Radiation Oncology |
| American Thoracic Society |
| Association for Molecular Pathology |
| British Lung Foundation |
| British Thoracic Society |
| Canadian Medical Association Infobase |
| Canadian Task Force on Preventive Health Care |
| Cancer Australia |
| Cancer Care Ontario |
| Cancer Control Alberta |
| Cancer Research UK |
| Care Quality Commission |
| College of American Pathologists |
| Core Outcome Measures in Effectiveness Trials (COMET) |
| Department of Health & Social Care |
| European Respiratory Society |
| European Society for Medical Oncology |
| European Society of Gastrointestinal Endoscopy |
| European Society of Thoracic Surgery |
| General Medical Council |
| Guidelines & Audit Implementation Network (GAIN) |
| Guidelines International Network (GIN) |
| Healthtalk Online |
| International Association for the Study of Lung Cancer |
| MacMillan Cancer Support |
| Medicines and Products Regulatory Agency (MHRA) |
| National Audit Office |
| National Cancer Intelligence Network |
| National Clinical Audit and Patient Outcomes Programme |
| National Health and Medical Research Council - Australia |
| National Institute for Health and Care Excellence (NICE) - published & in development guidelines |
| National Institute for Health and Care Excellence (NICE) - Topic Selection |
| NHS Choices |
| NHS Digital |
| NHS England |
| NICE Clinical Knowledge Summaries (CKS) |
| NICE Evidence Search |
| Office for National Statistics |
| Patient UK |
| PatientVoices |
| Public Health England |
| Quality Health |
| Royal College of Anaesthetists |
| Royal College of General Practitioners |
| Royal College of Midwives |
| Royal College of Nursing |
| Royal College of Pathologists |
| Royal College of Physicians |
| Royal College of Radiologists |
| Royal College of Surgeons |
| Scottish Government |
| Scottish Intercollegiate Guidelines Network (SIGN) |
| UK Data Service |
| US National Guideline Clearinghouse |
| Walsall community Health NHS Trust |
| Welsh Government |
Clinical search literature search strategy
Main searches
Bibliographic databases searched for the guideline
- Cochrane Database of Systematic Reviews – CDSR (Wiley)
- Cochrane Central Register of Controlled Trials – CENTRAL (Wiley)
- Database of Abstracts of Reviews of Effects – DARE (Wiley)
- Health Technology Assessment Database – HTA (Wiley)
- EMBASE (Ovid)
- MEDLINE (Ovid)
- MEDLINE Epub Ahead of Print (Ovid)
- MEDLINE In-Process (Ovid)
Identification of evidence for review questions
The searches were conducted between October 2017 and April 2018 for 9 review questions (RQ).
Searches were re-run in May 2018.
Where appropriate, in-house study design filters were used to limit the retrieval to, for example, randomised controlled trials. Details of the study design filters used can be found in section 3.
Search strategy
|
Medline Strategy, searched 26th February 2018 Database: Ovid MEDLINE(R) 1946 to Present with Daily Update Search Strategy: | |
|---|---|
| 1 | exp Lung Neoplasms/ |
| 2 | ((lung* or pulmonary or bronch*) adj3 (cancer* or neoplasm* or carcinoma* or tumo?r* or lymphoma* or metast* or malignan* or blastoma* or carcinogen* or adenocarcinoma* or angiosarcoma* or chrondosarcoma* or sarcoma* or teratoma* or microcytic*)).tw. |
| 3 | ((pancoast* or superior sulcus or pulmonary sulcus) adj4 (tumo?r* or syndrome*)).tw. |
| 4 | ((lung* or pulmonary or bronch*) adj4 (oat or small or non-small) adj4 cell*).tw. |
| 5 | (SCLC or NSCLC).tw. |
| 6 | or/1-5 |
| 7 | (N2* or cN2* or pN2* or ypN2* or T*N2* or N0-2* or IIIA* or cIIIA* or IIIB*).tw. |
| 8 | (stag* adj3 (three or III or four or IV or late* or advance*)).tw. |
| 9 | (stag* adj3 (“3” or “4”)).tw. |
| 10 | (local* advanc* adj3 (non-small or NSCLC)).tw. |
| 11 | LA-NSCLC.tw. |
| 12 | Mediastinum/ |
| 13 | Mediastinal Neoplasms/ |
| 14 | (mediastin* or subcarinal).tw. |
| 15 | or/7-14 |
| 16 | Thoracic Surgery/ |
| 17 | Thoracic Surgical Procedures/ |
| 18 | Pulmonary Surgical Procedures/ |
| 19 | Pneumonectomy/ |
| 20 | Thoracotomy/ |
| 21 | exp Thoracoscopy/ |
| 22 | ((lung* or pulmonary or bronch* or thorax or thorac*) adj4 (surg* or operation* or reoperation* or resection* or excision*)).tw. |
| 23 | (surg* adj1 resection*).tw. |
| 24 | (pneumonectom* or pneumoresect* or pulmonectom* or thoracotom* or pleuracotom* or pleurotom* or pleuroscop* or rethoracotom* or pneumolobectom* or segmentectom* or thoracoscop* or videothoracoscop* or bilobectom*).tw. |
| 25 | (EPP or PNE or VATS).tw. |
| 26 | (pleura* adj4 (endoscop* or incision*)).tw. |
| 27 | ((lung* or pulmonary or bronch*) adj4 lobect*).tw. |
| 28 | ((wedge or triangl*) adj4 (resect* or excision*)).tw. |
| 29 | or/16-28 |
| 30 | exp Chemoradiotherapy/ |
| 31 | (chemoradiotherap* or radiochemotherap* or chemoradiation*).tw. |
| 32 | (CRT or CRTx or CCRT or NCRT or RCTx or RT-CT or chemoRT).tw. |
| 33 | Combined Modality Therapy/ |
| 34 | (combine* adj4 modal* adj4 (treat* or therap* or regimen* or manag* or intervention*)).tw. |
| 35 | ((tri-modal* or trimodal* or multi-modal* or multimodal*) adj4 (treat* or therap* or regimen* or manag* or intervention*)).tw. |
| 36 | TMT.tw. |
| 37 | or/30-36 |
| 38 | 29 or 37 |
| 39 | 6 and 15 and 38 |
| 40 | Animals/ not Humans/ |
| 41 | 39 not 40 |
| 42 | limit 41 to english language |
Note: In-house RCT and systematic review filters were appended. No date limit was used due to additional terminology to that in the searches carried out in the 2011 guideline update.
Study Design Filters
| The MEDLINE SR, RCT, and observational studies filters are presented below. | |
|---|---|
| Systematic Review | |
| 1. | Meta-Analysis.pt. |
| 2. | Meta-Analysis as Topic/ |
| 3. | Review.pt. |
| 4. | exp Review Literature as Topic/ |
| 5. | (metaanaly$ or metanaly$ or (meta adj3 analy$)).tw. |
| 6. | (review$ or overview$).ti. |
| 7. | (systematic$ adj5 (review$ or overview$)).tw. |
| 8. | ((quantitative$ or qualitative$) adj5 (review$ or overview$)).tw. |
| 9. | ((studies or trial$) adj2 (review$ or overview$)).tw. |
| 10. | (integrat$ adj3 (research or review$ or literature)).tw. |
| 11. | (pool$ adj2 (analy$ or data)).tw. |
| 12. | (handsearch$ or (hand adj3 search$)).tw. |
| 13. | (manual$ adj3 search$).tw. |
| 14. | or/1-13 |
| 15. | animals/ not humans/ |
| 16. | 14 not 15 |
| RCT | |
| 1 | Randomized Controlled Trial.pt. |
| 2 | Controlled Clinical Trial.pt. |
| 3 | Clinical Trial.pt. |
| 4 | exp Clinical Trials as Topic/ |
| 5 | Placebos/ |
| 6 | Random Allocation/ |
| 7 | Double-Blind Method/ |
| 8 | Single-Blind Method/ |
| 9 | Cross-Over Studies/ |
| 10 | ((random$ or control$ or clinical$) adj3 (trial$ or stud$)).tw. |
| 11 | (random$ adj3 allocat$).tw. |
| 12 | placebo$.tw. |
| 13 | ((singl$ or doubl$ or trebl$ or tripl$) adj (blind$ or mask$)).tw. |
| 14 | (crossover$ or (cross adj over$)).tw. |
| 15 | or/1-14 |
| 16 | animals/ not humans/ |
| 17 | 15 not 16 |
| Observational | |
| 1 | Observational Studies as Topic/ |
| 2 | Observational Study/ |
| 3 | Epidemiologic Studies/ |
| 4 | exp Case-Control Studies/ |
| 5 | exp Cohort Studies/ |
| 6 | Cross-Sectional Studies/ |
| 7 | Controlled Before-After Studies/ |
| 8 | Historically Controlled Study/ |
| 9 | Interrupted Time Series Analysis/ |
| 10 | Comparative Study.pt. |
| 11 | case control$.tw. |
| 12 | case series.tw. |
| 13 | (cohort adj (study or studies)).tw. |
| 14 | cohort analy$.tw. |
| 15 | (follow up adj (study or studies)).tw. |
| 16 | (observational adj (study or studies)).tw. |
| 17 | longitudinal.tw. |
| 18 | prospective.tw. |
| 19 | retrospective.tw. |
| 20 | cross sectional.tw. |
| 21 | or/1-20 |
Health Economics literature search strategy
Sources searched to identify economic evaluations
- NHS Economic Evaluation Database – NHS EED (Wiley) last updated Apr 2015
- Health Technology Assessment Database – HTA (Wiley) last updated Oct 2016
- Embase (Ovid)
- MEDLINE (Ovid)
- MEDLINE In-Process (Ovid)
Search filters to retrieve economic evaluations and quality of life papers were appended to the review question search strategies. For some health economics strategies additional terms were added to the original review question search strategies (see sections 4.2, 4.3 and 4.4) The searches were conducted between October 2017 and April 2018 for 9 review questions (RQ).
Searches were re-run in May 2018.
Searches were limited to those in the English language. Animal studies were removed from results.
Economic evaluation and quality of life filters
| Medline Strategy | |
|---|---|
| Economic evaluations | |
| 1 | Economics/ |
| 2 | exp “Costs and Cost Analysis”/ |
| 3 | Economics, Dental/ |
| 4 | exp Economics, Hospital/ |
| 5 | exp Economics, Medical/ |
| 6 | Economics, Nursing/ |
| 7 | Economics, Pharmaceutical/ |
| 8 | Budgets/ |
| 9 | exp Models, Economic/ |
| 10 | Markov Chains/ |
| 11 | Monte Carlo Method/ |
| 12 | Decision Trees/ |
| 13 | econom$.tw. |
| 14 | cba.tw. |
| 15 | cea.tw. |
| 16 | cua.tw. |
| 17 | markov$.tw. |
| 18 | (monte adj carlo).tw. |
| 19 | (decision adj3 (tree$ or analys$)).tw. |
| 20 | (cost or costs or costing$ or costly or costed).tw. |
| 21 | (price$ or pricing$).tw. |
| 22 | budget$.tw. |
| 23 | expenditure$.tw. |
| 24 | (value adj3 (money or monetary)).tw. |
| 25 | (pharmacoeconomic$ or (pharmaco adj economic$)).tw. |
| 26 | or/1-25 |
| Quality of life | |
| 1 | “Quality of Life”/ |
| 2 | quality of life.tw. |
| 3 | "Value of Life”/ |
| 4 | Quality-Adjusted Life Years/ |
| 5 | quality adjusted life.tw. |
| 6 | (qaly$ or qald$ or qale$ or qtime$).tw. |
| 7 | disability adjusted life.tw. |
| 8 | daly$.tw. |
| 9 | Health Status Indicators/ |
| 10 | (sf36 or sf 36 or short form 36 or shortform 36 or sf thirtysix or sf thirty six or shortform thirtysix or shortform thirty six or short form thirtysix or short form thirty six).tw. |
| 11 | (sf6 or sf 6 or short form 6 or shortform 6 or sf six or sfsix or shortform six or short form six).tw. |
| 12 | (sf12 or sf 12 or short form 12 or shortform 12 or sf twelve or sftwelve or shortform twelve or short form twelve).tw. |
| 13 | (sf16 or sf 16 or short form 16 or shortform 16 or sf sixteen or sfsixteen or shortform sixteen or short form sixteen).tw. |
| 14 | (sf20 or sf 20 or short form 20 or shortform 20 or sf twenty or sftwenty or shortform twenty or short form twenty).tw. |
| 15 | (euroqol or euro qol or eq5d or eq 5d).tw. |
| 16 | (qol or hql or hqol or hrqol).tw. |
| 17 | (hye or hyes).tw. |
| 18 | health$ year$ equivalent$.tw. |
| 19 | utilit$.tw. |
| 20 | (hui or hui1 or hui2 or hui3).tw. |
| 21 | disutili$.tw. |
| 22 | rosser.tw. |
| 23 | quality of wellbeing.tw. |
| 24 | quality of well-being.tw. |
| 25 | qwb.tw. |
| 26 | willingness to pay.tw. |
| 27 | standard gamble$.tw. |
| 28 | time trade off.tw. |
| 29 | time tradeoff.tw. |
| 30 | tto.tw. |
| 31 | or/1-30 |
Health economics search strategy
|
Medline Strategy, searched 13th February 2018 Database: Ovid MEDLINE(R) 1946 to Present with Daily Update Search Strategy: | |
|---|---|
| 1 | Small Cell Lung Carcinoma/ |
| 2 | Carcinoma, Small Cell/ |
| 3 | SCLC.tw. |
| 4 | ((pancoast* or superior sulcus or pulmonary sulcus) adj4 (tumo?r* or syndrome*)).tw. |
| 5 | or/1-4 |
| 6 | ((small or oat or reserve or round) adj1 cell adj1 (lung* or pulmonary or bronch*) adj3 (cancer* or neoplasm* or carcinoma* or tumo?r* or lymphoma* or metast* or malignan* or blastoma* or carcinogen* or adenocarcinoma* or angiosarcoma* or chrondosarcoma* or sarcoma* or teratoma* or microcytic*)).tw. |
| 7 | (non adj1 small adj1 cell adj1 (lung* or pulmonary or bronch*) adj3 (cancer* or neoplasm* or carcinoma* or tumo?r* or lymphoma* or metast* or malignan* or blastoma* or carcinogen* or adenocarcinoma* or angiosarcoma* or chrondosarcoma* or sarcoma* or teratoma* or microcytic*)).tw. |
| 8 | 6 not 7 |
| 9 | 5 or 8 |
| 10 | exp Radiotherapy/ |
| 11 | Radiation Oncology/ |
| 12 | exp Radiography, Thoracic/ |
| 13 | radiotherapy.fs. |
| 14 | (radiotherap* or radiotreat* or roentgentherap* or radiosurg*).tw. |
| 15 | ((radiat* or radio* or irradiat* or roentgen or x-ray or xray) adj4 (therap* or treat* or repair* or oncolog* or surg*)).tw. |
| 16 | (RT or RTx or XRT or TRT or TCRT).tw. |
| 17 | or/10-16 |
| 18 | 9 and 17 |
| 19 | limit 18 to english language |
| 20 | Animals/ not Humans/ |
| 21 | 19 not 20 |
Appendix D. Evidence study selection
Appendix E. Clinical evidence tables
Download PDF (342K)
Appendix F. GRADE tables
Network meta-analyses1: chemoradiotherapy, surgery vs chemoradiotherapy vs chemotherapy, surgery
| Quality assessment | Effect estimate | Quality | |||||
|---|---|---|---|---|---|---|---|
| No of studies | Design | Risk of bias | Indirectness | Inconsistency | Imprecision | Summary of results (95% CI) | |
| Progression free life years at 4 years | |||||||
| 6 RCTs (Albain 2009, Eberhard 2015, Pless 2015, Girard 2009, Katakami 2012, van Meerbeeck 2007) | RCTs | Not Serious | Not Serious | Not Serious | Not Serious | CS vs CR: 0.00 (−0.21, 0.22) CRS vs CR: 0.25 (0.06,0.44) | High |
| Post progression life years at 4 years | |||||||
| 6 RCTs (as above) | RCTs | Not Serious | Not Serious | Not Serious | Not Serious | CS vs CR: −0.11 (−0.32,0.11) CRS vs CR: −0.18 (−0.28,−0.08) | High |
| Total life years at 4 years | |||||||
| 6 RCTs (as above) | RCTs | Not Serious | Not Serious | Not Serious | Serious2 | CS vs CR: −0.11 (−0.19,−0.03) CRS vs CR: 0.07 (−0.13,0.27) | Moderate |
| Odds ratio of being alive at 4 years | |||||||
| 6 RCTs (as above) | RCTs | Not Serious | Not Serious | Not Serious | Serious2 | CS vs CR: 1.18 (0.76,1.86) CRS vs CR: 1.28 (0.86,1.90) | Moderate |
| Progression free life years at 5 years | |||||||
| 5 RCTs (Albain 2009, Eberhard 2015, Pless 2015, Katakami 2012, van Meerbeeck 2007) | RCTs | Not Serious | Not Serious | Not Serious | Not Serious | CS vs CR: 0.01 (−0.27, 0.3) CRS vs CR: 0.38 (0.12,0.63) | High |
| Post progression life years at 5 years | |||||||
| 5 RCTs (as above) | RCTs | Not Serious | Not Serious | Not Serious | Not Serious | CS vs CR: −0.09 (−0.18, 0.01) CRS vs CR: −0.2 (−0.33,0.07) | High |
| Total life years at 5 years | |||||||
| 5 RCTs (as above) | RCTs | Not Serious | Not Serious | Not Serious | Serious2 | CS vs CR: −0.07 (−0.36, 0.22) CRS vs CR: 0.17 (−0.11,0.45) | Moderate |
| Odds ratio of being alive at 5 years | |||||||
| 5 RCTs (as above) | RCTs | Not Serious | Not Serious | Not Serious | Serious2 | CS vs CR: 1.32 (0.77, 2.14) CRS vs CR: 1.28 (0.83,1.92) | Moderate |
| Total adverse events of grade 3+ hazard ratio | |||||||
| 4 RCTs (Albain 2009, Eberhard 2015, Pless 2015, van Meerbeeck 2007) | RCTs | Not Serious | Not Serious | Not Serious | Not Serious | CR vs CRS: 1.24 (1.13,1.38) CS vs CRS: 1.39 (1.18,1.67) | High |
- 1
Effect sizes for CS vs CRS are not shown for outcomes other than total adverse event hazard ratio. This was the only outcome for which there was a statistically significant difference between CS and CRS.
- 2
Not possible to distinguish any meaningfully distinct treatment options in the network
Chemoradiotherapy, surgery vs chemoradiotherapy
| Quality assessment | No of patients | Effect estimate | Quality | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No of studies | Design | Risk of bias | Indirectness | Inconsistency | Imprecision | Chemoradio, surgery | Chemoradio | Summary of results (95% CI) | |
| Mortality: all-cause hazard ratio (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | HR 0.87 (0.69, 1.09) | Moderate |
| Adverse events grade 3 or above: leukopenia (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 0.87 (0.72, 1.05) | Moderate |
| Adverse events grade 3 or above: neutropenia (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 0.92 (0.72, 1.18) | Moderate |
| Adverse events grade 3 or above: anaemia (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Not serious | 202 | 194 | RR 0.53 (0.34, 0.82) | High |
| Adverse events grade 3 or above: thrombocytopenia (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 0.58 (0.31, 1.10) | Moderate |
| Adverse events grade 3 or above: worst haematologic toxicity per patient (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 0.90 (0.77, 1.05) | Moderate |
| Adverse events grade 3 or above: nausea and/or emesis (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Not serious | 202 | 194 | RR 0.44 (0.27, 0.71) | High |
| Adverse events grade 3 or above: neuropathy (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 1.37 (0.53, 3.53) | Moderate |
| Adverse events grade 3 or above: oesophagitis (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Not serious | 202 | 194 | RR 0.44 (0.27, 0.71) | High |
| Adverse events grade 3 or above: stomatitis and/or mucositis (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 1.15 (0.36, 3.71) | Moderate |
| Adverse events grade 3 or above: pulmonary (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Not serious | 202 | 194 | RR 0.58 (0.39, 0.87) | High |
| Adverse events grade 3 or above: other gastrointestinal or renal (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 1.37 (0.53, 3.53) | Moderate |
| Adverse events grade 3 or above: cardiac (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 1.07 (0.44, 2.57) | Moderate |
| Adverse events grade 3 or above: miscellaneous infection (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 0.72 (0.25, 2.04) | Moderate |
| Adverse events grade 3 or above: haemorrhage (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 0.96 (0.06, 15.25) | Moderate |
| Adverse events grade 3 or above: fatigue (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 1.17 (0.50, 2.77) | Moderate |
| Adverse events grade 3 or above: anorexia (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 0.41 (0.11, 1.57) | Moderate |
| Adverse events grade 3 or above: allergy (values greater than 1 favour chemoradio) | |||||||||
| 1 (Albain 2009) | RCT | Not serious | Not serious | N/A | Serious1 | 202 | 194 | RR 0.32 (0.03, 3.05) | Moderate |
- 3
95% CI of the effect size crosses the line of no effect
Chemoradiotherapy, surgery vs chemotherapy, surgery
| Quality assessment | No of people | Effect estimate | Quality | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No of studies | Design | Risk of bias | Indirectness | Inconsistency | Imprecision | Chemo, surgery | Chemoradiotherapy, surgery | Summary of results | |
| Mortality: all-cause hazard ratio (values below 1 favour chemoradiotherapy, surgery) | |||||||||
| 2 (Katakami 2012, Pless 2015) | RCT | Not serious | Not serious | Not serious | Serious1 | 149 | 138 | HR 0.94 (0.69, 1.27) | Moderate |
| Mortality: risk ratio for survival at 1 year (values below 1 favour chemoradiotherapy, surgery) | |||||||||
| 1 (Girard 2010) | RCT | Serious2 | Not serious | Not serious | Serious1 | 14 | 32 | RR 1.10 (0.89, 1.36) | Low |
| Mortality: risk ratio for survival at 2 years (values below 1 favour chemoradiotherapy, surgery) | |||||||||
| 1 (Girard 2010) | RCT | Serious2 | Not serious | Not serious | Serious1 | 14 | 32 | RR 0.87 (0.52, 1.46) | Low |
| Mortality: risk ratio for survival at 3 years (values below 1 favour chemoradiotherapy, surgery) | |||||||||
| 2 (Girard 2010, Katakami 2012) | RCT | Serious2 | Not serious | Serious4 | Serious1 | 42 | 60 | RR 0.76 (0.49, 1.18) | Very low |
| Adverse events grade 3 or above: stomatitis (values above 1 favour chemoradiotherapy, surgery) | |||||||||
| 1 (Pless 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 121 | 110 | RR 4.55 (0.54, 38.30) | Moderate |
| Adverse events grade 3 or above: dyspnoea (values above 1 favour chemoradiotherapy, surgery) | |||||||||
| 2 (Katakami 2012, Pless 2015) | RCT | Not serious | Not serious | Not serious | Serious1 | 149 | 138 | RR 8.19 (0.45, 150.38) | Moderate |
| Adverse events grade 3 or above: pneumonitis (values above 1 favour chemoradiotherapy, surgery) | |||||||||
| 1 (Girard 2010) | RCT | Serious2 | Not serious | Not serious | Serious1 | 14 | 32 | RR 0.73 (0.03, 16.97) | Low |
- 1
95% CI of the effect size crosses the line of no effect
- 2
Girard 2010: Randomisation was stratified by clinical centre and histological type (squamous cell carcinoma vs. others). However, the groups were not balanced in terms of gender or pN2/cN2. This might be because of the relatively low numbers of participants. Nevertheless, they were not balanced.
Chemotherapy, chemoradiotherapy + surgery vs chemotherapy, chemoradiotherapy boost
| Quality assessment | No of people | Effect estimate | Quality | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No of studies | Design | Risk of bias | Indirectness | Inconsistency | Imprecision | Chemo, chemorad + surgery | Chemo, chemorad boost | Summary of results (95% CI) | |
| Mortality: risk ratio for survival at 1 year (values over 1 favour chemo, chemorad + surgery) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 0.94 (0.81, 1.10) | Moderate |
| Mortality: risk ratio for survival at 2 years (values over 1 favour chemo, chemorad + surgery) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.07 (0.84, 1.37) | Moderate |
| Mortality: risk ratio for survival at 3 years (values over 1 favour chemo, chemorad + surgery) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.08 (0.75, 1.56) | Moderate |
| Mortality: risk ratio for survival at 4 years (values over 1 favour chemo, chemorad + surgery) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.23 (0.75, 2.04) | Moderate |
| Mortality: risk ratio for survival at 5 years (values over 1 favour chemo, chemorad + surgery) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.23 (0.69, 2.21) | Moderate |
| Mortality: risk ratio for survival at 6 years (values over 1 favour chemo, chemorad + surgery) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.12 (0.60, 2.08) | Moderate |
| Adverse events grade 3 or above: leukopenia (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.01 (0.78, 1.30) | Moderate |
| Adverse events grade 3 or above: anaemia (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.10 (0.47, 2.56) | Moderate |
| Adverse events grade 3 or above: thrombocytopenia (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.11 (0.45, 2.74) | Moderate |
| Adverse events grade 3 or above: nausea/vomiting (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.55 (0.63, 3.80) | Moderate |
| Adverse events grade 3 or above: neuropathy (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 0.99 (0.30, 3.28) | Moderate |
| Adverse events grade 3 or above: oesophagitis (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Not serious | 81 | 80 | RR 0.52 (0.27, 1.00) | High |
| Adverse events grade 3 or above: mucositis/stomatitis (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.48 (0.25, 8.63) | Moderate |
| Adverse events grade 3 or above: pulmonary (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.78 (0.62, 5.07) | Moderate |
| Adverse events grade 3 or above: other GI or renal (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.58 (0.54, 4.62) | Moderate |
| Adverse events grade 3 or above: cardiac (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.98 (0.37, 10.48) | Moderate |
| Adverse events grade 3 or above: miscellaneous infection (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 2.30 (0.62, 8.60) | Moderate |
| Adverse events grade 3 or above: fatigue (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 0.62 (0.21, 1.81) | Moderate |
| Adverse events grade 3 or above: pain (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.17 (0.65, 2.11) | Moderate |
| Dropout during treatment (values over 1 favour chemo, chemorad boost) | |||||||||
| 1 (Eberhardt 2015) | RCT | Not serious | Not serious | N/A | Serious1 | 81 | 80 | RR 1.65 (0.41, 6.66) | Moderate |
- 1
95% CI of the effect size crosses the line of no effect
Chemotherapy, surgery vs chemotherapy, radiotherapy
| Quality assessment | No of people | Effect estimate | Quality | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No of studies | Design | Risk of bias | Indirectness | Inconsistency | Imprecision | Chemo, surgery | Chemo, radio | Summary of results (95% CI) | |
| Mortality: all-cause hazard ratio (values greater than 1 favour chemo, radio) | |||||||||
| 1 (van Meerbeeck 2007) | RCT | Not serious | Not serious | N/A | Serious2 | 154 | 154 | HR 1.06 (0.85, 1.33) | Moderate |
| Mortality: risk ratio of being alive at 1 year (values greater than 1 favour chemo, surgery) | |||||||||
| 1 (Johnstone 2002) | RCT | Very serious1,3 | Not serious | N/A | Serious2 | 29 | 32 | RR 1.00 (0.69, 1.44) | Very low |
| Mortality: risk ratio of being alive at 2 years (values greater than 1 favour chemo, surgery) | |||||||||
| 1 (Johnstone 2002) | RCT | Very serious1,3 | Not serious | N/A | Serious2 | 29 | 32 | RR 1.30 (0.70, 2.44) | Very low |
| Mortality: risk ratio of being alive at 3 years (values greater than 1 favour chemo, surgery) | |||||||||
| 1 (Johnstone 2002) | RCT | Very serious1,3 | Not serious | N/A | Serious2 | 29 | 32 | RR 1.42 (0.61, 3.32) | Very low |
| Mortality: risk ratio of being alive at 4 years (values greater than 1 favour chemo, surgery) | |||||||||
| 1 (Johnstone 2002) | RCT | Very serious1,3 | Not serious | N/A | Serious2 | 29 | 32 | RR 0.95 (0.36, 2.49) | Very low |
| Mortality: risk ratio of treatment-related mortality | |||||||||
| 1 (Johnstone 2002) | RCT | Very serious1,3 | Not serious | N/A | Serious2 | 29 | 32 | RR 3.30 (0.14, 77.95) | Very low |
| Dropout during treatment | |||||||||
| 1 (van Meerbeeck 2007) | RCT | Serious1 | Not serious | N/A | Serious2 | 165 | 167 | HR 0.85 (0.37, 1.95) | Low |
- 1
Incomplete and selective reporting of data
- 2
95% CI of the effect size crosses the line of no effect
- 3
Some participants were not randomised and had different chemotherapy regimens
Chemotherapy, surgery vs radiotherapy
| Quality assessment | No of people | Effect estimate | Quality | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No of studies | Design | Risk of bias | Indirectness | Inconsistency | Imprecision | Chemo, surgery | Radio | Summary of results (95% CI) | |
| Mortality: all-cause | |||||||||
| 1 (Shepherd 1998) | RCT | Very serious1,2 | Not serious | N/A | Very serious3,4 | 16 | 15 | Median survival 18.7 months in chemo, surgery arm (12.9 – 32) Median survival 16.2 months in radio arm (10.7 – 32.3)5 | Very low |
| Mortality: all-cause hazard ratio | |||||||||
| 1 (Stephens 20015) | RCT | Very serious6 | Not serious | N/A | Serious7 | 24 | 24 | HR 0.91 (0.49, 1.70) | Very low |
| Mortality: treatment-related deaths | |||||||||
| 1 (Stephens 20015) | RCT | Serious1 | Not serious | N/A | Serious7 | 24 | 24 | RR 5.00 (0.25, 98.96) | Low |
| Adverse events grade 2 or above: lethargy | |||||||||
| 1 (Stephens 20015) | RCT | Serious1 | Not serious | N/A | Serious7 | 24 | 24 | RR 1.44 (0.77, 2.72) | Low |
| Dropout during treatment (values greater than 1 favour radiotherapy) | |||||||||
| 1 (Shepherd 1998) | RCT | Very serious1,2 | Not serious | N/A | Very serious4 | 16 | 15 | RR 3.75 (0.47, 29.87) | Very low |
| Dropout during treatment (values greater than 1 favour radiotherapy) | |||||||||
| 1 (Stephens 20015) | RCT | Serious1 | Not serious | N/A | Serious7 | 24 | 24 | RR 0.11 (0.01, 1.96) | Low |
- 1
Incomplete and selective reporting of data
- 2
Method of randomisation not given and arms were not balanced at baseline
- 3
The 95% CIs for the median values overlap
- 4
Sample size is 25 to 40. Therefore, downgraded once for imprecision
- 5
However, according to the survival chart, follow-up was only 21 months for radiotherapy (~34% were still alive) and 32 months for chemotherapy, surgery (30% were still alive)
- 6
High risk of bias
- 7
95% CI of the effect size crosses the line of no effect
Chemotherapy, chemoradiotherapy, surgery, radiotherapy vs chemotherapy, surgery, radiotherapy
| Quality assessment | No of people | Effect estimate | Quality | ||||||
|---|---|---|---|---|---|---|---|---|---|
| No of studies | Design | Risk of bias | Indirectness | Inconsistency | Imprecision | Chemo, chemorad, surgery, radio | Chemo, surgery, radio | Summary of results (95% CI) | |
| Mortality: all-cause hazard ratio (values greater than 1 favour chemo, chemorad, surgery, radio) | |||||||||
| 1 (Thomas 2008) | RCT | Very serious1 | Very serious2 | N/A | Serious3 | 264 | 260 | HR 0.91 (0.49, 1.70) | Very low |
| Mortality: treatment related: all (values greater than 1 favour chemo, surgery, radio) | |||||||||
| 1 (Thomas 2008) | RCT | Very serious1 | Very serious2 | N/A | Serious3 | 264 | 260 | RR 1.12 (0.57, 2.19) | Very low |
| Mortality: treatment related: fatal events after neutropenia caused by chemotherapy (values greater than 1 favour chemo, surgery, radio) | |||||||||
| 1 (Thomas 2008) | RCT | Very serious1 | Very serious2 | N/A | Serious3 | 264 | 260 | RR 0.66 (0.11, 3.90) | Very low |
| Mortality: treatment related: oesophagitis (values greater than 1 favour chemo, surgery, radio) | |||||||||
| 1 (Thomas 2008) | RCT | Very serious1 | Very serious2 | N/A | Serious3 | 206 | 187 | RR 2.72 (0.11, 66.48) | Very low |
| Mortality: treatment related: pneumonitis (values greater than 1 favour chemo, surgery, radio) | |||||||||
| 1 (Thomas 2008) | RCT | Very serious1 | Very serious2 | N/A | Serious3 | 206 | 187 | RR 0.08 (0.00, 1.48) | Very low |
| Mortality: treatment related: surgical mortality (values greater than 1 favour chemo, surgery, radio) | |||||||||
| 1 (Thomas 2008) | RCT | Very serious1 | Very serious2 | N/A | Serious3 | 142 | 154 | RR 2.01 (0.83, 4.91) | Very low |
| Adverse events grade 3 or above: haemotoxicity (values greater than 1 favour chemo, surgery, radio) | |||||||||
| 1 (Thomas 2008) | RCT | Very serious1 | Very serious2 | N/A | Not serious | 206 | 187 | RR 18.16 (2.46, 133.96) | Very low |
| Adverse events grade 3 or above: oesophagitis (values greater than 1 favour chemo, surgery, radio) | |||||||||
| 1 (Thomas 2008) | RCT | Very serious1 | Very serious2 | N/A | Serious3 | 206 | 187 | RR 5.06 (2.32, 11.03) | Very low |
| Adverse events grade 3 or above: pneumonitis (values greater than 1 favour chemo, surgery, radio) | |||||||||
| 1 (Thomas 2008) | RCT | Very serious1 | Very serious2 | N/A | Not serious | 206 | 187 | RR 0.21 (0.06, 0.72) | Very low |
| Adverse events: peri-operative complications (values greater than 1 favour chemo, surgery, radio) | |||||||||
| 1 (Thomas 2008) | RCT | Very serious1 | Very serious2 | N/A | Serious3 | 142 | 154 | RR 1.51 (0.86, 2.64) | Very low |
- 1
Incomplete and selective reporting of data. Over 20% of participants were lost to follow-up with regards to adverse events data
- 2
Participants who were N2 were in the minority: chemo, chemoradio, surgery = 17%; chemo, surgery = 12%. 349 of 524 patients (67%) had stage IIIB disease and comprised a substantial proportion of 113 of 524 patients (22%) with pathologically confirmed N3 disease
- 3
95% CI of the effect size crosses the line of no effect
Appendix G. Meta-analyses
Randomised controlled trials
Chemoradiotherapy, surgery vs chemotherapy, surgery
Appendix H. Excluded Studies
Excluded clinical studies
| Study | Title | Reason for exclusion |
|---|---|---|
| Billiet 2016 | Postoperative radiotherapy for lung cancer: Is it worth the controversy? | Paper on postoperative radiotherapy, not tri-modality treatment. |
| Chen 2018 | Comparing the benefits of chemoradiotherapy and chemotherapy for resectable stage III A/N2 non-small cell lung cancer: a meta-analysis | The studies used in this systematic review were checked to ensure that we included all relevant ones. |
| Cheng 2005 | Predicting efficacy of neoadjuvant cheomotherapy on resectable stage IIIA non-small cell lung cancer by multi-gene expressions | This study is not written in English. In addition, it is on the prognostic value of gene expressions |
| Guberina 2017 | Heart dose exposure as prognostic marker after radiotherapy for resectable stage IIIA/B non-small-cell lung cancer: secondary analysis of a randomized trial | This is a secondary analysis of Eberhardt 2015. However, the data was not analysed as an RCT. Both arms were placed into the same group |
| Pass 1992 | Randomized trial of neoadjuvant therapy for lung cancer: interim analysis | The comparison of ‘surgery, radiotherapy vs chemotherapy, surgery, chemotherapy’ is not in the protocol |
| Pezzetta 2005 | Comparison of neoadjuvant cisplatin-based chemotherapy versus radiochemotherapy followed by resection for stage III (N2) NSCLC | Retrospective study |
| Pottgen 2017 | Definitive radiochemotherapy versus surgery within multimodality treatment in stage III non-small cell lung cancer (NSCLC) - a cumulative meta-analysis of the randomized evidence | Not a systematic review. This is a metaanalysis of selected studies. This meta-analysis also includes a study that is conference proceedings. The studies used in this meta-analysis were checked to ensure that we included all relevant ones. |
| Shah 2011 | Induction chemoradiotherapy is not superior to induction chemotherapy alone in patients with stage IIIA(N2) non-small cell lung cancer: a systematic review and meta-analysis | Conference proceedings. This abstract has a lot of information. However, this systematic review used 2 studies that were abstracts (conference proceedings). It also includes 2 retrospective studies. The studies used in this systematic review were checked to ensure that we included all relevant ones. |
| Shah 2012 | Induction chemoradiation is not superior to induction chemotherapy alone in stage IIIA lung cancer | Systematic review contains mostly retrospective studies and conference proceedings. This systematic review used 2 studies that were abstracts (conference proceedings). It also includes 3 retrospective studies. The studies used in this systematic review were checked to ensure that we included all relevant ones. |
| Sorensen 2013 | Surgery for NSCLC stages T1-3N2M0 having preoperative pathologically verified N2 involvement: a prospective randomized multinational phase III trial by the Nordic Thoracic Oncology Group | Conference proceedings |
Excluded economic studies
| Paper | Primary reason for exclusion |
|---|---|
| Bongers, M.L., de Ruysscher, D., Oberije, C., Lambin, P., Uyl-de Groot, C.A., Belderbos, J. and Coupe, V.M., 2017. Model-based cost-effectiveness of conventional and innovative chemo-radiation in lung cancer. International journal of technology assessment in health care, 33(6), pp.681-690. | Not a cost-utility paper that met the PICOS criteria. |
| Louie, A.V., Rodrigues, G.B., Palma, D.A. and Senan, S., 2014. Measuring the population impact of introducing stereotactic ablative radiotherapy for stage I non-small cell lung cancer in Canada. The oncologist, 19(8), pp.880-885. | Not a cost-utility paper that met the PICOS criteria. |
Appendix I. References
Clinical Studies - Included
- Albain K S, Swann R S, Rusch V W, Turrisi A T, 3rd, Shepherd F A, Smith C, Chen Y, Livingston R B, Feins R H, Gandara D R, Fry W A, Darling G, Johnson D H, Green M R, Miller R C, Ley J, Sause W T, and Cox J D (2009) Radiotherapy plus chemotherapy with or without surgical resection for stage III non-small-cell lung cancer: a phase III randomised controlled trial. Lancet374(9687), 379–86 [PMC free article: PMC4407808] [PubMed: 19632716]
- Eberhardt W E, Pottgen C, Gauler T C, Friedel G, Veit S, Heinrich V, Welter S, Budach W, Spengler W, Kimmich M, Fischer B, Schmidberger H, De Ruysscher, D, Belka C, Cordes S, Hepp R, Lutke-Brintrup D, Lehmann N, Schuler M, Jockel K H, Stamatis G, and Stuschke M (2015) Phase III Study of Surgery Versus Definitive Concurrent Chemoradiotherapy Boost in Patients With Resectable Stage IIIA(N2) and Selected IIIB Non-Small-Cell Lung Cancer After Induction Chemotherapy and Concurrent Chemoradiotherapy (ESPATUE). Journal of Clinical Oncology33(35), 4194–201 [PubMed: 26527789]
- Girard N, Mornex F, Douillard J Y, Bossard N, Quoix E, Beckendorf V, Grunenwald D, Amour E, and Milleron B (2010) Is neoadjuvant chemoradiotherapy a feasible strategy for stage IIIA-N2 non-small cell lung cancer? Mature results of the randomized IFCT-0101 phase II trial. Lung Cancer69(1), 86–93 [PubMed: 19879013]
- Johnstone D W, Byhardt R W, Ettinger D, and Scott C B(2002) Phase III study comparing chemotherapy and radiotherapy with preoperative chemotherapy and surgical resection in patients with non-small-cell lung cancer with spread to mediastinal lymph nodes (N2); final report of RTOG 89-01. Radiation Therapy Oncology Group. International Journal of Radiation Oncology, Biology, and Physics54(2), 365–9 [PubMed: 12243809]
- Katakami N, Tada H, Mitsudomi T, Kudoh S, Senba H, Matsui K, Saka H, Kurata T, Nishimura Y, and Fukuoka M(2012) A phase 3 study of induction treatment with concurrent chemoradiotherapy versus chemotherapy before surgery in patients with pathologically confirmed N2 stage IIIA nonsmall cell lung cancer (WJTOG9903). Cancer118(24), 6126–35 [PubMed: 22674529]
- Leo F, De Pas, T, Catalano G, Piperno G, Curigliano G, Solli P, Veronesi G, Petrella F, and Spaggiari L(2007) Re: Randomized controlled trial of resection versus radiotherapy after induction chemotherapy in stage IIIA-N2 non-small cell lung cancer. Journal of the National Cancer Institute99(15), 1210; author reply 1210–1 [PubMed: 17652281]
- Pless M, Stupp R, Ris H B, Stahel R A, Weder W, Thierstein S, Gerard M A, Xyrafas A, Fruh M, Cathomas R, Zippelius A, Roth A, Bijelovic M, Ochsenbein A, Meier U R, Mamot C, Rauch D, Gautschi O, Betticher D C, Mirimanoff R O, Peters S, and Group Sakk Lung Cancer Project (2015) Induction chemoradiation in stage IIIA/N2 non-small-cell lung cancer: a phase 3 randomised trial.[Erratum appears in Lancet. 2015 Sep 12;386(9998):1040; PMID: 26382996]. Lancet386(9998), 1049–56 [PubMed: 26275735]
- Shepherd F A, Johnston M R, Payne D, Burkes R, Deslauriers J, Cormier Y, de Bedoya, L D, Ottaway J, James K, and Zee B(1998) Randomized study of chemotherapy and surgery versus radiotherapy for stage IIIA non-small-cell lung cancer: a National Cancer Institute of Canada Clinical Trials Group Study. British Journal of Cancer78(5), 683–5 [PMC free article: PMC2063048] [PubMed: 9744511]
- Stephens R J, Girling D J, Hopwood P, Thatcher N, Medical Research Council Lung Cancer Working, and Party (2005) A randomised controlled trial of pre-operative chemotherapy followed, if feasible, by resection versus radiotherapy in patients with inoperable stage T3, N1, M0 or T1-3, N2, M0 non-small cell lung cancer. Lung Cancer49(3), 395–400 [PubMed: 15908042]
- Thomas M, Rube C, Hoffknecht P, Macha H N, Freitag L, Linder A, Willich N, Hamm M, Sybrecht G W, Ukena D, Deppermann K M, Droge C, Riesenbeck D, Heinecke A, Sauerland C, Junker K, Berdel W E, Semik M, German Lung Cancer Cooperative, and Group (2008) Effect of preoperative chemoradiation in addition to preoperative chemotherapy: a randomised trial in stage III non-small-cell lung cancer. Lancet Oncology9(7), 636–48 [PubMed: 18583190]
- van Meerbeeck, J P, Kramer G W, Van Schil P E, Legrand C, Smit E F, Schramel F, Tjan-Heijnen V C, Biesma B, Debruyne C, van Zandwijk, N, Splinter T A, Giaccone G, European Organisation for, Research, Treatment of Cancer-Lung Cancer, and Group (2007) Randomized controlled trial of resection versus radiotherapy after induction chemotherapy in stage IIIA-N2 non-small-cell lung cancer. Journal of the National Cancer Institute99(6), 442–50 [PubMed: 17374834]
Clinical studies – Excluded
- Billiet C, Peeters S, Decaluwe H, Vansteenkiste J, Mebis J, and Ruysscher D D(2016) Postoperative radiotherapy for lung cancer: Is it worth the controversy?. Cancer Treatment Reviews51, 10–18 [PubMed: 27788387]
- Chen Y, Peng X, Zhou Y, Xia K, and Zhuang W(2018) Comparing the benefits of chemoradiotherapy and chemotherapy for resectable stage III A/N2 non-small cell lung cancer: a meta-analysis. World Journal of Surgical Oncology16(1), 8 [PMC free article: PMC5771204] [PubMed: 29338734]
- Cheng C, Wu Yl, Gu Lj, Chen G, Weng Ym, Feng Wn, and Zhong Wz(2005) Predicting efficacy of neoadjuvant cheomotherapy on resectable stage IIIA non-small cell lung cancer by multi-gene expressions. Ai zheng [Chinese journal of cancer]24(7), 846–849 [PubMed: 16004813]
- Guberina M, Eberhardt W, Stuschke M, Gauler T, Heinzelmann F, Cheufou D, Kimmich M, Friedel G, Schmidberger H, Darwiche K, Jendrossek V, Schuler M, Stamatis G, and Pottgen C(2017) Heart dose exposure as prognostic marker after radiotherapy for resectable stage IIIA/B non-small-cell lung cancer: secondary analysis of a randomized trial. Annals of Oncology28(5), 1084–1089 [PubMed: 28453703]
- Pass H I, Pogrebniak H W, Steinberg S M, Mulshine J, and Minna J(1992) Randomized trial of neoadjuvant therapy for lung cancer: interim analysis. Annals of Thoracic Surgery53(6), 992–8 [PubMed: 1317697]
- Pezzetta E, Stupp R, Zouhair A, Guillou L, Taffe P, von Briel, C, Krueger T, and Ris H B (2005) Comparison of neoadjuvant cisplatin-based chemotherapy versus radiochemotherapy followed by resection for stage III (N2) NSCLC.[Erratum appears in Eur J Cardiothorac Surg. 2005 Aug;28(2):368]. European Journal of Cardio-Thoracic Surgery27(6), 1092–8 [PubMed: 15896624]
- Pottgen C, Eberhardt W, Stamatis G, and Stuschke M(2017) Definitive radiochemotherapy versus surgery within multimodality treatment in stage III non-small cell lung cancer (NSCLC) - a cumulative meta-analysis of the randomized evidence. Oncotarget8(25), 41670–41678 [PMC free article: PMC5522187] [PubMed: 28415831]
- Shah Aa, Berry Mf, Tzao C, Rajgor D, Pietrobon R, and D’Amico Ta(2011) Induction chemoradiotherapy is not superior to induction chemotherapy alone in patients with stage IIIA(N2) non-small cell lung cancer: a systematic review and meta-analysis. Journal of thoracic oncology. 6(6suppl. 2), S1578–s1579
- Shah A A, Berry M F, Tzao C, Gandhi M, Worni M, Pietrobon R, and D’Amico T A(2012) Induction chemoradiation is not superior to induction chemotherapy alone in stage IIIA lung cancer. Annals of Thoracic Surgery93(6), 1807–12 [PubMed: 22632486]
- Sorensen Jb, Ravn J, Pilegaard Hk, Palshof T, Sundstrom S, Bergman B, Jakobsen Jn, Aasebo U, Hansen O, Meldgaard P, Soerensen Bt, Jakobsen E, Jonsson P, Ryberg M, Salo J, Haverstad R, and Riska H(2013) Surgery for NSCLC stages T1-3N2M0 having preoperative pathologically verified N2 involvement: a prospective randomized multinational phase III trial by the Nordic Thoracic Oncology Group. Journal of clinical oncology31(15suppl. 1),
Health Economic studies – Included
None
Health Economic studies – Excluded
- Bongers, M.L., de Ruysscher, D., Oberije, C., Lambin, P., Uyl-de Groot, C.A., Belderbos, J. and Coupe, V.M., 2017. Model-based cost-effectiveness of conventional and innovative chemo-radiation in lung cancer. International journal of technology assessment in health care, 33(6), pp.681–690. [PubMed: 29122046]
- Louie, A.V., Rodrigues, G.B., Palma, D.A. and Senan, S., 2014. Measuring the population impact of introducing stereotactic ablative radiotherapy for stage I non-small cell lung cancer in Canada. The oncologist, 19(8), pp.880–885. [PMC free article: PMC4122471] [PubMed: 24951606]
Appendix J. Network Meta-analysis
Background
Evidence synthesis was performed for survival outcomes and for adverse events associated with the three interventions of interest; chemoradiotherapy (CR), chemotherapy and surgery (CS) and chemoradiotherapy and surgery (CRS). In this review, all studies provided Kaplan Meier curves for progression free survival (PFS) and overall survival (OS). Visual inspection of the Kaplan Meier curves revealed that the proportional hazards assumption did not appear to hold, and so traditional pooling of hazards ratios was not considered appropriate. Furthermore, the shapes of the survival curves were different across studies, suggesting that it was not appropriate to synthesise the evidence under an assumption of a single parametric model. A non-parametric approach to evidence synthesis was therefore required.
An alternative measure of treatment effect for time-to-event outcomes is the difference in the restricted mean survival time (RMST) [1], where RMST is the mean survival time accrued from randomisation up to T years. RMST can be estimated by the area under the survival curve (AUC) up to time T, and the treatment effect estimated as the difference in AUCs between treatments. This measure does not assume proportional hazards and can be calculated regardless of the curve fitted to the data, including directly from the Kaplan-Meier curve, and so can allow for different survival distributions across studies.
In addition, the PFS and OS outcomes are related, because OS is a sum of progression free survival (PFS) and post-progression survival (PPS). Joint modelling of OS and PFS, where the synthesis model is given to PFS and PPS, ensures that predictions from the model conform to the natural constraint that OS is always greater than PFS.
We begin by describing the Network Meta-Analysis (NMA) methods used to estimate the treatment effects on the area under the Kaplan Meier curves for OS and PFS jointly. We then describe how these estimates can be combined with external evidence on longer-term survival to estimate mean time in PFS and PPS on each treatment. Because the non-parametric approach taken means that it is not straightforward to apply discounting in the economic model, we describe how the NMA is adapted to obtain discounted mean survival times required for the economic model. We also describe the NMA model used to synthesis evidence on adverse events. We then describe how we selected models on the basis of model fit and checked for inconsistency in the NMAs. We then present the results from the NMAs and the estimates to be inputted into the economic model.
Synthesising the Clinical Evidence: Methods
Data extraction
Data was extracted from the Kaplan Meier curves using a validated algorithm that makes use of the digitized curves as well as data on the numbers at risk and total number of events [2]. For each treatment group within each study, this produces a set of individual patient data (survival times and censor times) that produce Kaplan-Meier curves similar to those published. This was done for both the PFS and OS curves.
Calculating the Area Under the Kaplan Meier Curves
Kaplan Meier curves were fitted to the extracted data using the survfit function from the survival package in R (v. 3.4.2)[3, 4]. The area under the Kaplan Meier curves from randomisation t0 = 0 to a truncated follow up time tT was calculated as a Reimann sum
All studies report Kaplan Meier curves up until T=5 years, with the exception of Girard (2009) which reports up to T=4 years. We use T=5 years to estimate differences in the restricted mean survival time in the base-case (which excludes Girard 2009) and use T=4 years in a sensitivity analysis (which includes all studies).
The areas under the Kaplan Meier curves for each RCT are provided in Table 9.
Table 9. Trial data for evidence synthesis (Treatment 1=CR, 2=CS and 3=CRS)
Correlation between AUCs for PFS and OS
The AUCs for progression free and overall survival are correlated because the AUC for OS must be greater than for PFS. We estimated this correlation using non-parametric bootstrapping, constrained to samples where the AUC for OS was greater than that for PFS [6]. These correlations are provided in Table 9.
Network meta-analysis for PFS and OS
Let and be the estimated AUC up to T years for study i, arm k, for PFS and OS respectively, with covariance matrix Vi,k for the PFS and OS AUC(T) outcomes. We assume the AUCs follows a Bivariate Normal likelihood:
Normal(0,10000) prior distributions are given to the trial-specific baselines , and for the treatment effects on the AUCs , . In the case of random effects models, the between study standard deviations σPFS, σPPS for the treatment effects on AUC for PFS and PPS were assigned Uniform(0,5) priors.
For an assumed restricted mean PFS time over T-years on reference treatment 1 in a UK population, , we can derive the mean time spent progression free up to T-years for treatment k in a UK population:
Similarly, for an assumed mean PPS time over T-years on reference treatment 1 in a UK population, , we can derive the mean time spent in PPS for treatment k in a UK population:
Predicted Mean Survival Time
To predict lifetime mean survival time beyond the truncated study periods (T = 4 or 5 years), required extrapolation using long-term survival data from an external source. Let C be the area under the Kaplan Meier curve obtained from an appropriate external source of data conditional on having survived T-years, which can be interpreted as life-expectancy conditional on surviving the first T years.
Assuming that all those who are alive at T-years are progression free, and remain progression free thereafter, the mean time spent progression free for treatment k in a UK population is:
Under the assumption that those who survive to T-years remain progression-free, no further time spent in PPS is obtained after T-years so that:
Probability of Surviving up to T years, Sk (T)
The probability of surviving up to T years (T = 4 or 5 years) for each treatment group was pooled across trials in a separate NMA. Let be the estimated survival probability at T-years in study i, arm k, with standard error sei,k. Assuming the survival probabilities at T-years follow a Normal likelihood:
Trial-specific baseline and treatment effects for probability of survival up to 4 or 5 years were assigned Normal(0,10000) prior distributions. In the case of random effects models, the between study standard deviation σS was assigned a Uniform(0,5) prior.
External Survival Data
To estimate mean survival time beyond T years conditional on surviving to T years, we made use of survival data collected from the Surveillance Epidemiology and End Results (SEER) cancer incidence database [8]. A subset of the incidence database was extracted to ensure patients matched those include in the NMA in terms of age at diagnosis (30 – 79 years), cancer site (lung), and stage of cancer (IIIA-N2). Exact selection criteria are given in Section 8. This produced a dataset of 23,602 patients with a maximum observed survival time of 25.7 years. Since the SEER dataset was used to predict survival beyond the truncated study period, we were interested in the SEER data conditional on patients being alive at the end of the truncated study period. After conditioning survival on being alive at 4 and 5 years after diagnosis, data on the remaining 3,703 and 2,865 patients, respectively, were used to calculate the area under the conditional SEER Kaplan Meier curves using the methods described in Section 2.2. Several parametric survival curves were fitted to the SEER data: exponential, Weibull, gamma, log-normal, Gompertz, and log-logistic. The fit of each curve was compared using the Akaike information criterion (AIC) and Bayesian information criterion (BIC). For the SEER data conditional on being alive at 5 years, a Weibull distribution with a shape parameter of 0.88 and scale parameter of 7.37 gave the lowest AIC (Figure 1). For the SEER data conditional on being alive at 4 years, a Weibull distribution with a shape parameter of 0.85 and scale parameter of 6.88 gave the lowest AIC.
Additional Requirements for Economic Model
Discounting Area Under the Kaplan Meier Curves
The economic evaluation required the area under the Kaplan Meier curve to be discounted at an annual rate of 3.5% [7]. The discounted area (up to T years) for each treatment group within each trial, as well as the SEER dataset, was calculated as
The standard error of, and correlation between, the discounted area under the Kaplan Meier curves for PFS and OS was calculated using non-parametric bootstrapping, constrained to samples where the OS curve was greater than the PFS curve [6]. The discounted areas under the Kaplan Meier curves for each RCT are provided in Table 10.
Table 10. Discounted area under the curve data required for economic modelling
To compute discounted costs of death beyond the truncated study periods (T = 4 or 5 years), a parametric survival curve was used to model the conditional SEER data, as described in the External Survival Data section above.
Discounting one-off costs
The economic model includes one-off costs for progression events, which also require discounting. The non-parametric approach provides the total number of events by time T, but does not give the breakdown of these events into 1-year time periods required for discounting. To obtain the proportion of total events falling in each 1-year period, let yi,k,s be the survival probability at s years with standard error sei,k,s, in arm k of study i. We assume the survival probabilities follow a Normal likelihood:
Let ρi,k,s be the proportion of events that have occurred by T = 5-years in study i, arm k, that occur in year s. Then the proportion surviving to 4-years, πi,k,4, is the proportion surviving to 5 years, plus for those experiencing an event by year 5 the proportion of those events that occur in the 5th year:
Table 11. Proportion of events occurring each year (Treatment 1=CR, 2=CS and 3=CRS)
Model Critique
Assessing model fit
The posterior mean of the residual deviance, which measures the magnitude of the differences between the observed data and the model predictions of the data, was used to assess the goodness of fit of each model [12]. Smaller values are preferred, and in a well-fitting model the posterior mean residual deviance should be close to the number of data points in the network (each study arm contributes 1 data point) [12].
In addition to comparing how well the models fit the data using the posterior mean of the residual deviance, models were compared using the deviance information criterion (DIC). This is equal to the sum of the posterior mean deviance and the effective number of parameters, and thus penalizes model fit with model complexity [12]. Lower values are preferred and differences of at least 5 points were considered meaningful [12].
Assessing heterogeneity and inconsistency
Heterogeneity concerns the differences in treatment effects between trials within each treatment contrast, while consistency concerns the differences between the direct and indirect evidence informing the treatment contrasts [9, 10].
Heterogeneity is assessed by comparing the fit of fixed and random effects NMA models. The fixed effect model assumes that all trials are estimating the same treatment effect, regardless of any differences in the conduct of the trials, populations, or treatments. The random effects NMA model on the other hand accounts for any differences in treatment effects between trials, that are beyond sampling error, by assuming a distribution of study-specific treatment effects with a pooled mean and between-study standard deviation. The estimated between study standard deviation in treatment effects is also inspected to assess heterogeneity.
Inconsistency was assessed by comparing the fit of the chosen consistency model (fixed or random effects) to an “inconsistency”, or unrelated mean effects, model [9, 10]. The latter is equivalent to having separate, unrelated, meta-analyses for every pairwise contrast, with a common variance parameter assumed in the case of random effects models. Note that inconsistency can only be assessed when there are closed loops of direct evidence on 3 treatments that are informed by at least 3 distinct trials [11].
Network meta-analysis: Results of Clinical Evidence Synthesis
5-year Follow-up
Five studies presented survival data up to 5-years, and a network diagram summarizing the evidence is given in Figure 2
Model fit statistics for the area under the Kaplan Meier curves up to 5-years, as well as the probability of survival are given in Table 12. Convergence was satisfactory for the fixed effect model after a burn-in of 20,000 iterations and results are based on a further 40,000 samples on two chains. For the random effects model, convergence was satisfactory after a burn-in of 30,000 iterations and results are based on a further 60,000 samples on two chains.
Table 12. Model fit statistics based on 5-year follow-up data
There were no meaningful differences between the fixed and random effects models in terms of the posterior mean residual deviance and DIC for both NMAs (Table 12). The box plots of the posterior deviance values for each study arm in Figure 3 and Figure 4 show that the area under the Kaplan Meier curves and probability of survival up to 5 years are predicted fairly well by both models. The simpler fixed effect model was therefore selected in the base-case.
No evidence of inconsistency was found, with model fit (posterior mean residual deviance) similar for the consistency and inconsistency (unrelated means) fixed effect models, and a lower DIC for the consistency model (Table 13). The area below the line of equality in Figure 5 highlights where the inconsistency model better predicted data points, and any improvement is minimal.
There is evidence to suggest that chemoradiotherapy + surgery is more effective in increasing progression free life years at 5-year follow-up compared to chemoradiotherapy alone, while there is no evidence to suggest the effect of chemotherapy + surgery is any different from chemoradiotherapy (Figure 6A, Table 14). There is also evidence to suggest that chemoradiotherapy + surgery improves progression free life years compared to chemotherapy + surgery (posterior median difference in RMST: 0.34 (95% CrI: 0.02, 0.65)) and it ranked the most effective intervention in increasing progression free life years (Table 14).
In terms of post progression life years at 5-year follow-up, there was not enough to conclude that any one intervention was better than any other although point estimates favoured chemoradiotherapy (Figure 6B, Table 14). There was not enough evidence to suggest any of the three treatments were different from each other in terms of improving total life years at 5-year follow-up, which is the sum of the progression free and post progression life years (Figure 6C, Table 14).
Chemotherapy + surgery and chemoradiotherapy + surgery appear to be more likely to improve the odds of being alive at 5-years compared to chemoradiotherapy alone, but there is not enough evidence to infer the direction of effects with certainty (Figure 6D, Table 14).
Figure 6Forest plots of (A) differences in restricted mean progression free life years at 5-years follow-up relative to chemoradiotherapy, (B) differences in restricted mean post progression life years at 5-years follow-up relative to chemoradiotherapy, (C) differences in restricted mean total life years at 5-years follow-up relative to chemoradiotherapy, and (D) odds ratios of being alive at 5-years follow-up relative to chemoradiotherapy. Results are presented as the posterior median and 95% credible intervals. Abbreviations: CR – chemoradiotherapy, CS – chemotherapy + surgery, CRS – chemoradiotherapy + surgery
A. Difference in Restricted Mean Progression Free Life Years at 5 Years
B. Difference in Restricted Mean Post Progression Life Years at 5 Years
C. Difference in Restricted Mean Total Life Years at 5 Years
Sensitivity analyses
As part of an assessment of the sensitivity of the results to the selected follow-up time, we also synthesised data based on a shorter follow-up period of 4-years, which allowed the inclusion of all 6 studies, including Girard 2009. Model fit statistics for the fixed and random effects models based on the 4-year follow-up data are given in Table 15. Convergence was satisfactory for the fixed effect model after a burn-in of 20,000 iterations and results are based on a further 40,000 samples on two chains. For the random effects model, convergence was satisfactory after a burn-in of 30,000 iterations and results are based on a further 60,000 samples on two chains.
Table 15. Model fit statistics based on 4-year follow-up data
There were no meaningful differences between the fixed and random effects models in terms of the posterior mean residual deviance and DIC (Table 15). The plots of the posterior deviance values for each study arm in Figure 7 show that the probability of survival up to 4 years in Girard 2009 is not predicted well and this study is a possible outlier. Fitting a random effects model did not help in the prediction of data points in this study (Figure 8). The simpler fixed effect model is therefore preferred.
No evidence of inconsistency was found through comparison of the consistency and inconsistency random effects models, as little difference was observed between the fit of the models (Table 16). The area below the line of equality in Figure 9 highlights where the inconsistency model better predicted data points, but any improvements were minimal.
Treatment effects estimated by the fixed and random effects models based on the 4- and 5-year follow up data are presented in Figure 10. The point estimates of the treatment effects are similar, and the width of the credible intervals reflect that random effects models estimate the treatment effects with more uncertainty, and that there is additional data included in the 4-dataset compared with the 5-year dataset.
Noting that
- the model fit assessment supports the use of the fixed effect model in both datasets,
- the assumption that non-progressors by T-years do not progress (are “cured”) is more reasonable at 5-years than at 4-years,
- the 5-year dataset excludes the Girard (2009) study, which seems to be an outlier and is based on small numbers
Figure 10Forest plots of fixed and random effects estimates at 5- and 4-year follow up for (A) differences in restricted mean progression free life years at T-years follow-up relative to chemoradiotherapy, (B) differences in restricted mean post progression life years at T-years follow-up relative to chemoradiotherapy, (C) differences in restricted mean total life years at T-years follow-up relative to chemoradiotherapy, and (D) odds ratios of being alive at T-years follow-up relative to chemoradiotherapy. Abbreviations: CR – chemoradiotherapy, CS – chemotherapy + surgery, CRS – chemoradiotherapy + surgery
A. Difference in Restricted Mean Progression Free Life Years
B. Difference in Restricted Mean Post Progression Life Years
Results: Inputs for Economic Model
Discounted Area Under the Kaplan Meier Curves and Probability of Survival
The fit of the NMA models based on the discounted AUC was also assessed and were in line with the results presented in the Network meta-analysis section above. For both the 4-year and 5-year follow-up data, there were no meaningful differences between the fit of the fixed and random effects models (Table 17), and thus the fixed effect model was preferred.
Table 17. Model fit statistics based on 5-year follow-up data, discounted at 3.5% annual rate
Similarly, the fit of the consistency and inconsistency models for both 4- and 5-year follow-up data were compared (Table 18). There is no evidence of inconsistency as no meaningful differences were found in the fit of the models for both datasets. The area below the line of equality in Figure 11 and Figure 12 highlights where the inconsistency model better predicted data points, but any improvements were minimal.
Proportion of Events Occurring each Year
The proportion of events occurring each year pooled across studies is given in Table 19. The estimated proportions are similar across the 5-year and 4-year follow-up datasets.
NMA for Adverse Events
The base case approach used in the economic model for adverse events used pairwise meta-analyses but data then became available that allowed us to fit an NMA for use in sensitivity analyses.
The studies had reported adverse events heterogeneously; in some studies the reporting was comprehensive and in others scant or no details were available. Furthermore, events were classified heterogeneously across studies, being grouped under narrow or broad classes that made event-specific pooling difficult. The committee decided that adverse events should be included in the economic model if possible and we agreed an aggregate approach with them. This involved grouping all adverse events of grade 3+ as homogenously requiring one hospital admission, but having no long term clinical effects or detriment to quality of life. The committee thought it possible that grade 4 adverse events would affect quality of life but these occurred to sparsely to be meaningfully included in the model. Because of the wide disparity between the frequency of adverse events reported among the studies, we selected Pless 2015, Eberhardt 2015, Albain 2009 and van Meerbeeck 2007 for the analysis. These studies were the largest and best conducted studies in the network and had reported event rates that the committee found credible. The data from van Meerbeeck was not reported in the published paper but provided to us upon request by the EORTC, who hold the trial data. We obtained the person years at risk by multiplying the total number of patients in each arm by the mean AUC for total life years at 5 years. The data are in Table 20.
Table 20. Adverse Event NMA Input Data
We assumed that adverse events were treatment related and therefore that it was appropriate to assume a homogenous follow-up time. Since this meant that we did not have to account for variable study endpoints in our pooling of the data, we selected a Poisson likelihood, log link NMA model and copied the code directly from NICE TSD2 (Dias, 2011). The results of the fixed and random effects models are in Table 21. Models were run using 50,000 burn-in iterations and 50,000 iterations to generate the posterior distributions.
Table 21. Adverse Event NMA Results
The DIC for the random effects model was not more than 3-5 points lower than the fixed effects model so we preferred it in the base case. The results show that both CR and CS are associated with more adverse events than CRS.
As discussed in the economic modelling report (Appendix J), the point estimates of the NMA data agreed well with the pairwise estimates of adverse events.
NMA Progressions that are deaths
Data from three trials (Pless 2015, Albain 2009 and van Meerbeeck 2007) provided information on progressions that were deaths for 797 at risk patients across three treatments. The denominator was the total number of people that had progressed or died at 5 years and the numerator was the number of people who had died without progression. Of the constituent studies, Pless 2015 was the smallest whilst van Meerbeeck 2007 and Albain 2009 were the largest.
Table 22. Progressions That Are Deaths NMA Input Data
We selected a binomial likelihood, logit link NMAs for this data, using both a fixed effects and random effects models and copied the code directly from NICE TSD2 (Dias, 2011). The results (expressed as log-odds ratios of progression occurring as the first event) of this model are in Table 23. Models were run using 50,000 burn-in iterations and 50,000 iterations to generate the posterior distributions.
Table 23. Progressions That Are Deaths NMA Results
The DIC for the fixed effects model was just under 1.3 points lower than the random effects model so we preferred it in the base case. The results show that both CS and CRS are associated with more progressions that are deaths than CR because the credible intervals for the log-odds ratios do not cross 0. There was no difference between CS and CRS. This finding has clinical plausibility as the interventions including a surgical component are more invasive than CR alone.
References and Code
References
- 1.
- Royston, P. and M.K.B.Parmar, Restricted mean survival time: an alternative to the hazard ratio for the design and analysis of randomized trials with a time-to-event outcome. BMC Medical Research Methodology, 2013. 13: p. 152–152. [PMC free article: PMC3922847] [PubMed: 24314264]
- 2.
- Guyot, P., et al, Enhanced secondary analysis of survival data: reconstructing the data from published Kaplan-Meier survival curves. BMC Medical Research Methodology, 2012. 12: p. 9. [PMC free article: PMC3313891] [PubMed: 22297116]
- 3.
- Therneau, T.M. and P.M.Grambsch, A Package for Survival Analysis in S. 2015.
- 4.
- R Core Team, R: A language and environment for statistical computing. 2017, R Foundation for Statistical Computing: Vienna, Austria.
- 5.
- Klein, J.P. and M.L.Moeschberger, Survival Analysis: Techniques for Censored and Truncated Data. 2nd Edition ed. 2003, New York: Springer-Verlag.
- 6.
- Efron, B. and R.J.Tibshiranie, An introduction to the bootstrap. 1993, New York: Chapman & Hall.
- 7.
- National Institute for Health and Clinical Excellence, The guidelines Manual (November 2012). Available from http://publications
.nice .org.uk/the-guidelines-manual-pmg6. 2012, National Institute of Health and Clinical Excellence: London. [PubMed: 27905714] - 8.
- Surveillance Epidemiology and End Results (SEER) Program (www
.seer.cancer.gov), SEER*Stat Database: Incidence - SEER 9 Regs Research Data, Nov 2017 Sub (1973-2015)<Katrina/Rita Population Adjustment> - Linked To County Attributes - Total U.S., 1969-2016 Counties, National Cancer Institute, DCCPS, Surveillance Research Program, released April 2018, based on the November 2017 submission. - 9.
- Dias, S., et al, NICE DSU Technical Support Document 4: Inconsistency in networks of evidence based on randomised controlled trials, in Technical Support Document. 2011. [PubMed: 27466656]
- 10.
- Dias, S., et al, Evidence Synthesis for Decision Making 4: Inconsistency in networks of evidence based on randomized controlled trials. Medical Decision Making, 2013. 33: p. 641–656. [PMC free article: PMC3704208] [PubMed: 23804508]
- 11.
- van Valkenhoef, G., et al, Automated generation of node-splitting models for assessment of inconsistency in network meta-analysis. Research Synthesis Methods, 2016. 7: p. 80–93. [PMC free article: PMC5057346] [PubMed: 26461181]
- 12.
- Spiegelhalter, D.J., et al, Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society (B), 2002. 64(4): p. 583–616.
Code
SEER dataset
Selection criteria:
{Age at Diagnosis.Age recode with <1 year olds} = '30-34 years','35-39 years','40-44 years','45-49 years','50-54 years','55-59 years','60-64 years','65-69 years','70-74 years','75-79 years'
AND ({Site and Morphology.CS Schema v0204+} = 'Lung'
OR {Site and Morphology.CS Schema - AJCC 6th Edition} = 'Lung')
AND ({Stage - AJCC.Derived AJCC Stage Group, 7th ed (2010+)} = 'IIIA'
OR {Stage - AJCC.Derived AJCC Stage Group, 6th ed (2004+)} = 'IIIA'
OR {Stage - AJCC.AJCC stage 3rd edition (1988-2003)} = ' 31'
OR {Stage - AJCC.SEER modified AJCC stage 3rd (1988-2003)} = ' 31')
AND ({Stage - TNM.Derived AJCC N, 7th ed (2010+)} = 'N2','N2a','N2b','N2c'
OR {Stage - TNM.Derived AJCC N, 6th ed (2004+)} = 'N2','N2a','N2b','N2c'
OR {Stage - TNM.N value - based on AJCC 3rd (1988-2003)} = 'N2')
NMA Model for Adverse Events – Fixed Effects
# Poisson likelihood, log link
# Fixed effects model for multi-arm trials
model{ # *** PROGRAM STARTS
for(i in 1:ns){ # LOOP THROUGH STUDIES
mu[i] ~ dnorm(0,.0001) # vague priors for all trial baselines
for (k in 1:na[i]) { # LOOP THROUGH ARMS
r[i,k] ~ dpois(theta[i,k]) # Poisson likelihood
theta[i,k] <- lambda[i,k]*E[i,k] # event rate * exposure
log(lambda[i,k]) <- mu[i] + d[t[i,k]] - d[t[i,1]] # model for linear predictor
dev[i,k] <- 2*((theta[i,k]-r[i,k]) + r[i,k]*log(r[i,k]/theta[i,k])) #Deviance contribution
}
resdev[i] <- sum(dev[i,1:na[i]]) # summed residual deviance contribution for this trial
}
totresdev <- sum(resdev[]) #Total Residual Deviance
d[1]<-0 # treatment effect is zero for reference treatment
for (k in 2:nt){ d[k] ~ dnorm(0,.0001) } # vague priors for treatment effects
sd ~ dunif(0,5) # vague prior for between-trial SD
tau <- pow(sd,-2) # between-trial precision = (1/between-trial variance)
# pairwise HRs and LHRs for all possible pair-wise comparisons, if nt>2
for (c in 1:(nt-1)) {
for (k in (c+1):nt) {
lhr[c,k] <- (d[k]-d[c])
log(hr[c,k]) <- lhr[c,k]
}
}
} # *** PROGRAM ENDS
list(ns=4, nt=3)
t[,1] r[,1] E[,1] t[,2] r[,2] E[,2] na[]
2 182 285.2 3 141 299.52 2
3 482 434.3 1 608 409.34 2
1 137 214.4 3 150 230.04 2
1 98 321.75 2 108 298.93 2
END
#chain 1
list(d=c( NA, 0, 0), mu=c(0, 0, 0, 0))
#chain 2
list(d=c( NA, -1, 1), mu=c(-3, -3, -3, -3))
#chain 3
list(d=c( NA, 2, 2), mu=c(-3, 5, -1, -3))
NMA Model for Adverse Events - Random Effects
# Poisson likelihood, log link
# Random effects model for multi-arm trials
model{ # *** PROGRAM STARTS
for(i in 1:ns){ # LOOP THROUGH STUDIES
w[i,1] <- 0 # adjustment for multi-arm trials is zero for control arm
delta[i,1] <- 0 # treatment effect is zero for control arm
mu[i] ~ dnorm(0,.0001) # vague priors for all trial baselines
for (k in 1:na[i]) { # LOOP THROUGH ARMS
r[i,k] ~ dpois(theta[i,k]) # Poisson likelihood
theta[i,k] <- lambda[i,k]*E[i,k] # failure rate * exposure
log(lambda[i,k]) <- mu[i] + delta[i,k] # model for linear predictor
dev[i,k] <- 2*((theta[i,k]-r[i,k]) + r[i,k]*log(r[i,k]/theta[i,k])) #Deviance contribution
}
resdev[i] <- sum(dev[i,1:na[i]]) # summed residual deviance contribution for this trial
for (k in 2:na[i]) { # LOOP THROUGH ARMS
delta[i,k] ~ dnorm(md[i,k],taud[i,k]) # trial-specific LOR distributions
md[i,k] <- d[t[i,k]] - d[t[i,1]] + sw[i,k] # mean of LOR distributions (with multi-arm trial correction)
taud[i,k] <- tau *2*(k-1)/k # precision of LOR distributions (with multi-arm trial correction)
w[i,k] <- (delta[i,k] - d[t[i,k]] + d[t[i,1]]) # adjustment for multi-arm RCTs
sw[i,k] <- sum(w[i,1:k-1])/(k-1) # cumulative adjustment for multi-arm trials
}
}
totresdev <- sum(resdev[]) #Total Residual Deviance
d[1]<-0 # treatment effect is zero for reference treatment
for (k in 2:nt){ d[k] ~ dnorm(0,.0001) } # vague priors for treatment effects
sd ~ dunif(0,5) # vague prior for between-trial SD
tau <- pow(sd,-2) # between-trial precision = (1/between-trial variance)
# pairwise HRs and LHRs for all possible pair-wise comparisons, if nt>2
for (c in 1:(nt-1)) {
for (k in (c+1):nt) {
lhr[c,k] <- (d[k]-d[c])
log(hr[c,k]) <- lhr[c,k]
}
}
} # *** PROGRAM ENDS
list(ns=4, nt=3)
t[,1] r[,1] E[,1] t[,2] r[,2] E[,2] na[]
2 182 285.2 3 141 299.52 2
3 482 434.3 1 608 409.34 2
1 137 214.4 3 150 230.04 2
1 98 321.75 2 108 298.93 2
END
#chain 1
list(d=c( NA, 0, 0), sd=1, mu=c(0, 0, 0, 0))
#chain 2
list(d=c( NA, -1, 1), sd=4, mu=c(-3, -3, -3, -3))
#chain 3
list(d=c( NA, 2, 2), sd=2, mu=c(-3, 5, -1, -3))
R code to calculate (undiscounted and discounted) area under the Kaplan Meier curves, along with correlation between the areas under PFS and OS curves and standard error based on non-parametric bootstrap sampling
##Load survival package
library("survival")
#########################################################################
## Function to calculate area under a Kaplan Meier curve
## Required Input:
## data - with column names:
## "stime" (survival time for each patient),
## "event" (1 if patient experienced event, 0 if patient censored),
## "treat" (code for treatment patient received)
## rmean - time to restrict curve to
## Outputs: AUC restricted to 'rmean' years and its standard error
#########################################################################
my.AUC<-function(data,rmean){
fit<-survfit(Surv(stime,event)~1,data=data)
surv.stats<-summary(fit,print.rmean=TRUE,rmean=rmean)$table[5:6]
surv.stats
}
################################################################################
## Function to calculate area and discounted area under a Kaplan Meier curve
## Required Input:
## data - with column names:
## "stime" (survival time for each patient),
## "event" (1 if patient experienced event, 0 if patient censored),
## "treat" (code for treatment patient received)
## - note should only be 1 treatment in data
## max.time - time to restrict curve to
## dis.fac - discount factor, 1/(1+annual rate)
## Outputs: AUC and discounted AUC restricted to 'rmean' years
################################################################################
my.disc.AUC<-function(data,max.time=5,disc.fac=1/1.035){
#Fit Kaplan Meier curve to data
fit<-survfit(Surv(stime,event)~1,data=data)
#Calculate AUC in each one-year time interval
#Check to see if any patient experienced event at the end of a year
#If so, calculate AUC up to that time point
#If not, calculate AUC based on time at which an event was last observed before end of year
time<-0:max.time
X<-match(fit$time,time)
X<-X[-which(is.na(X))]
if(length(X)==0){time=time}else{time=time[-X]}
sum.fit<-summary(fit)
#Set up data required to calculate AUC in each one-year time interval
my.tab<-data.frame(time=sum.fit$time,
n.risk=sum.fit$n.risk,
n.event=sum.fit$n.event,
survival=sum.fit$surv,
std.err=sum.fit$std.err,
time.diff=rep(NA,length(sum.fit$time)),
AUC=rep(NA,length(sum.fit$time)))
#Add in lines for end of year time point to calculate AUC
temp.tab<-data.frame(time=time,
n.risk=rep(NA,length(time)),
n.event=rep(0,length(time)),
survival=c(1,rep(NA,length(time)-1)),
std.err=rep(NA,length(time)),
time.diff=rep(NA,length(time)),
AUC=rep(NA,length(time)))
my.tab<-rbind(my.tab,temp.tab)
my.tab<-my.tab[order(my.tab$time),]
#Make sure there are no time points beyond desired cut-off
test<-length(which(my.tab$time>max.time))>0
if(test){my.tab<-my.tab[-which(my.tab$time>max.time),]}else{my.tab<-my.tab}
#Calculate AUC between observed time points
for(i in 1:(length(time)-1)){
row.ind<-which(my.tab$time==time[i+1])
my.tab$survival[row.ind]=my.tab$survival[row.ind-1]
}
for(j in 2:length(my.tab[,1])){
my.tab$time.diff[j]<-my.tab$time[j]-my.tab$time[j-1]
my.tab$AUC[j]<-my.tab$survival[j-1]*my.tab$time.diff[j]
}
#Which rows contain end of year data
time.ind<-which(match(my.tab$time,0:max.time)!="NA")
#Calculate and output the AUC and discounted AUC in each one year time interval
undisc.AUC<-matrix(nrow=max.time,ncol=2)
disc.AUC<-matrix(nrow=max.time,ncol=2)
undisc.AUC[,1]<-1:max.time
disc.AUC[,1]<-1:max.time
for(k in 1:max.time){
undisc.AUC[k,2]<-sum(my.tab$AUC[(time.ind[k]+1):time.ind[k+1]])
disc.AUC[k,2]<-sum(my.tab$AUC[(time.ind[k]+1):time.ind[k+1]])*(disc.fac^(k-1))
}
t(rbind(undisc.AUC,disc.AUC))
}
##################################################################################
## Calculate SE of discounted AUC, correlation between AUC of PFS and OS curves via bootstrapping
##################################################################################
#Prepare tables to record AUC and Discounted AUC
#AUC at 5 years
AUC.tab.5<-matrix(ncol=24,nrow=5)
colnames(AUC.tab.5)<-c("t1","t2","PFS1.boot","OS1.boot","sePFS1.boot","seOS1.boot","corr1",
"PFS2.boot","OS2.boot","sePFS2.boot","seOS2.boot","corr2",
"S1","seS1","S2","seS2",
"PFS1","OS1","sePFS1","seOS1",
"PFS2","OS2","sePFS2","seOS2")
#Discounted AUC at 5 years
disc.AUC.tab.5<-matrix(ncol=20,nrow=5)
colnames(disc.AUC.tab.5)<-c("t1","t2","PFS1.boot","OS1.boot","sePFS1.boot","seOS1.boot","corr1",
"PFS2.boot","OS2.boot","sePFS2.boot","seOS2.boot","corr2",
"S1","seS1","S2","seS2",
"PFS1","OS1","PFS2","OS2")
#Load data for PFS and OS curves
data.pfs <- read.csv("filename.csv", stringsAsFactors=FALSE)
data.os <- read.csv("filename.csv", stringsAsFactors=FALSE)
#######################################################################
### Bootstrap each curve, for each treatment and outcome separately
#######################################################################
time.horizon<-5 #Cut off time (e.g., 5 years)
B<-5000 #Number of bootstrap samples
#Subset data in first treatment group
treat.num1<-sort(unique(data.pfs$treat))[1]
data.pfs1<-subset(data.pfs,treat==treat.num1)
data.os1<-subset(data.os,treat==treat.num1)
dim(data.pfs1)[1] #check number of patients
dim(data.os1)[1] #check number of patients - should equal above
#Create empty matrices to fill in for bootstrapping
boot.auc.pfs1<-matrix(nrow=B,ncol=(2*time.horizon)+2)
colnames(boot.auc.pfs1)<-c(paste(rep("AUC",time.horizon),1:time.horizon,sep="."),
paste(rep("dAUC",time.horizon),1:time.horizon,sep="."),
"AUC","dAUC")
boot.auc.os1<-matrix(nrow=B,ncol=(2*time.horizon)+2)
colnames(boot.auc.os1)<-c(paste(rep("AUC",time.horizon),1:time.horizon,sep="."),
paste(rep("dAUC",time.horizon),1:time.horizon,sep="."),
"AUC","dAUC")
#Set the seed
set.seed(1234)
#Bootstrap data, throw out bootstrap samples where OS curve is lower than PFS curve
i<-1
k<-0 #counter for discards
while(i<(B+1)){
#Calculate number of patients reporting PFS and OS
samp.pfs<-dim(data.pfs1)[1]
samp.os<-dim(data.os1)[1]
inds1<-sample(1:samp.pfs,replace=TRUE)
inds2<-sample(1:samp.os,replace=TRUE)
boot.data.pfs1<-data.pfs1[inds1[1:dim(data.pfs1)[1]],]
boot.data.os1<-data.os1[inds2[1:dim(data.os1)[1]],]
#Fit KM curves to resampled data
fit.pfs<-survfit(Surv(stime,event)~treat,data=boot.data.pfs1)
fit.os<-survfit(Surv(stime,event)~treat,data=boot.data.os1)
#Check to see if P(OS) >= P(PFS)
surv.test<-rep(NA,length(summary(fit.os)$time))
for(j in 1:length(summary(fit.os)$time)){
time.test<-which(summary(fit.os)$time[j]>=summary(fit.pfs)$time)
if(length(time.test)==0){
surv.test[j]<-FALSE
} else{
surv.test[j]<-summary(fit.os)$surv[j]>=summary(fit.pfs)$surv[max(time.test)]
}
}
surv.test.test<-sum(1*(surv.test=="FALSE"),na.rm=TRUE)
if(surv.test.test==0){
boot.auc.pfs1[i,1:(2*time.horizon)]<-my.disc.AUC(boot.data.pfs1,max.time=time.horizon)[2,]
boot.auc.pfs1[i,((2*time.horizon)+1):((2*time.horizon)+2)]<-c(sum(boot.auc.pfs1[i,1:time.horizon]),sum(boot.auc.pfs1[i,(time.horizon+1):(2*time.horizon)]))
boot.auc.os1[i,1:(2*time.horizon)]<-my.disc.AUC(boot.data.os1,max.time=time.horizon)[2,]
boot.auc.os1[i,((2*time.horizon)+1):((2*time.horizon)+2)]<-c(sum(boot.auc.os1[i,1:time.horizon]),sum(boot.auc.os1[i,(time.horizon+1):(2*time.horizon)]))
i<-i+1
} else {
i<-i
k<-k+1
}
}
#Number of samples thrown away
k
#Record results, fill in tables
AUC.tab.5[study.num,"t1"]<-treat.num1
disc.AUC.tab.5[study.num,"t1"]<-treat.num1
AUC.tab.5[study.num,"PFS1.boot"]<-mean(boot.auc.pfs1[,((2*time.horizon)+1)])
disc.AUC.tab.5[study.num,"PFS1.boot"]<-mean(boot.auc.pfs1[,((2*time.horizon)+2)])
AUC.tab.5[study.num,"sePFS1.boot"]<-sd(boot.auc.pfs1[,((2*time.horizon)+1)])
disc.AUC.tab.5[study.num,"sePFS1.boot"]<-sd(boot.auc.pfs1[,((2*time.horizon)+2)])
AUC.tab.5[study.num,"OS1.boot"]<-mean(boot.auc.os1[,((2*time.horizon)+1)])
disc.AUC.tab.5[study.num,"OS1.boot"]<-mean(boot.auc.os1[,((2*time.horizon)+2)])
AUC.tab.5[study.num,"seOS1.boot"]<-sd(boot.auc.os1[,((2*time.horizon)+1)])
disc.AUC.tab.5[study.num,"seOS1.boot"]<-sd(boot.auc.os1[,((2*time.horizon)+2)])
AUC.tab.5[study.num,"corr1"]<-cor(boot.auc.pfs1[,((2*time.horizon)+1)],boot.auc.os1[,((2*time.horizon)+1)])
disc.AUC.tab.5[study.num,"corr1"]<-cor(boot.auc.pfs1[,((2*time.horizon)+2)],boot.auc.os1[,((2*time.horizon)+2)])
fit.os1<-survfit(Surv(stime,event)~1,data=data.os1)
AUC.tab.5[study.num,"S1"]<-summary(fit.os1,time=time.horizon)$surv
AUC.tab.5[study.num,"seS1"]<-summary(fit.os1,time=time.horizon)$std.err
disc.AUC.tab.5[study.num,"S1"]<-summary(fit.os1,time=time.horizon)$surv
disc.AUC.tab.5[study.num,"seS1"]<-summary(fit.os1,time=time.horizon)$std.err
AUC.tab.5[study.num,"PFS1"]<-my.AUC(data.pfs1,rmean=5)[1]
AUC.tab.5[study.num,"sePFS1"]<-my.AUC(data.pfs1,rmean=5)[2]
AUC.tab.5[study.num,"OS1"]<-my.AUC(data.os1,rmean=5)[1]
AUC.tab.5[study.num,"seOS1"]<-my.AUC(data.os1,rmean=5)[2]
disc.AUC.tab.5[study.num,"PFS1"]<-sum(my.disc.AUC(data.pfs1,max.time=5,disc.fac=1/1.035)[2,6:10])
disc.AUC.tab.5[study.num,"OS1"]<-sum(my.disc.AUC(data.os1,max.time=5,disc.fac=1/1.035)[2,6:10])
#Save a copy of results from each bootstrapped sample
write.csv(boot.auc.pfs1,"filename pfs treat 1.csv")
write.csv(boot.auc.os1,"filename os treat 1.csv")
######################################
#Subset data in first treatment group
treat.num2<-sort(unique(data.pfs$treat))[2]
data.pfs2<-subset(data.pfs,treat==treat.num2)
data.os2<-subset(data.os,treat==treat.num2)
dim(data.pfs2)[1] #check number of patients
dim(data.os2)[1] #check number of patients - should equal above
#Create empty matrices to fill in for bootstrapping
boot.auc.pfs2<-matrix(nrow=B,ncol=(2*time.horizon)+2)
colnames(boot.auc.pfs2)<-c(paste(rep("AUC",time.horizon),1:time.horizon,sep="."),
paste(rep("dAUC",time.horizon),1:time.horizon,sep="."),
"AUC","dAUC")
boot.auc.os2<-matrix(nrow=B,ncol=(2*time.horizon)+2)
colnames(boot.auc.os2)<-c(paste(rep("AUC",time.horizon),1:time.horizon,sep="."),
paste(rep("dAUC",time.horizon),1:time.horizon,sep="."),
"AUC","dAUC")
#Set the seed
set.seed(1234)
#Bootstrap data, throw out bootstrap samples where OS curve is lower than PFS curve
i<-1
k<-0 #counter for discards
while(i<(B+1)){
#Calculate number of patients reporting PFS and OS
samp.pfs<-dim(data.pfs2)[1]
samp.os<-dim(data.os2)[1]
inds1<-sample(1:samp.pfs,replace=TRUE)
inds2<-sample(1:samp.os,replace=TRUE)
boot.data.pfs2<-data.pfs2[inds1[1:dim(data.pfs2)[1]],]
boot.data.os2<-data.os2[inds2[1:dim(data.os2)[1]],]
#Fit KM curves to resampled data
fit.pfs<-survfit(Surv(stime,event)~treat,data=boot.data.pfs2)
fit.os<-survfit(Surv(stime,event)~treat,data=boot.data.os2)
#Check to see if P(OS) > P(PFS)
surv.test<-rep(NA,length(summary(fit.os)$time))
for(j in 1:length(summary(fit.os)$time)){
time.test<-which(summary(fit.os)$time[j]>=summary(fit.pfs)$time)
#Added this ifelse statement on 22 January 2019 to account for cases where first OS event happened before first PFS event
if(length(time.test)==0){
surv.test[j]<-FALSE
} else{
surv.test[j]<-summary(fit.os)$surv[j]>=summary(fit.pfs)$surv[max(time.test)]
}
}
surv.test.test<-sum(1*(surv.test=="FALSE"),na.rm=TRUE)
if(surv.test.test==0){
boot.auc.pfs2[i,1:(2*time.horizon)]<-my.disc.AUC(boot.data.pfs2,max.time=time.horizon)[2,]
boot.auc.pfs2[i,((2*time.horizon)+1):((2*time.horizon)+2)]<-c(sum(boot.auc.pfs2[i,1:time.horizon]),sum(boot.auc.pfs2[i,(time.horizon+1):(2*time.horizon)]))
boot.auc.os2[i,1:(2*time.horizon)]<-my.disc.AUC(boot.data.os2,max.time=time.horizon)[2,]
boot.auc.os2[i,((2*time.horizon)+1):((2*time.horizon)+2)]<-c(sum(boot.auc.os2[i,1:time.horizon]),sum(boot.auc.os2[i,(time.horizon+1):(2*time.horizon)]))
i<-i+1
} else {
i<-i
k<-k+1
}
}
#Number of samples thrown away
k
#Record results, fill in tables
AUC.tab.5[study.num,"t2"]<-treat.num2
disc.AUC.tab.5[study.num,"t2"]<-treat.num2
AUC.tab.5[study.num,"PFS2.boot"]<-mean(boot.auc.pfs2[,((2*time.horizon)+1)])
disc.AUC.tab.5[study.num,"PFS2.boot"]<-mean(boot.auc.pfs2[,((2*time.horizon)+2)])
AUC.tab.5[study.num,"sePFS2.boot"]<-sd(boot.auc.pfs2[,((2*time.horizon)+1)])
disc.AUC.tab.5[study.num,"sePFS2.boot"]<-sd(boot.auc.pfs2[,((2*time.horizon)+2)])
AUC.tab.5[study.num,"OS2.boot"]<-mean(boot.auc.os2[,((2*time.horizon)+1)])
disc.AUC.tab.5[study.num,"OS2.boot"]<-mean(boot.auc.os2[,((2*time.horizon)+2)])
AUC.tab.5[study.num,"seOS2.boot"]<-sd(boot.auc.os2[,((2*time.horizon)+1)])
disc.AUC.tab.5[study.num,"seOS2.boot"]<-sd(boot.auc.os2[,((2*time.horizon)+2)])
AUC.tab.5[study.num,"corr2"]<-cor(boot.auc.pfs2[,((2*time.horizon)+1)],boot.auc.os2[,((2*time.horizon)+1)])
disc.AUC.tab.5[study.num,"corr2"]<-cor(boot.auc.pfs2[,((2*time.horizon)+2)],boot.auc.os2[,((2*time.horizon)+2)])
fit.pfs2<-survfit(Surv(stime,event)~1,data=data.pfs2)
fit.os2<-survfit(Surv(stime,event)~1,data=data.os2)
AUC.tab.5[study.num,"S2"]<-summary(fit.os2,time=time.horizon)$surv
AUC.tab.5[study.num,"seS2"]<-summary(fit.os2,time=time.horizon)$std.err
disc.AUC.tab.5[study.num,"S2"]<-summary(fit.os2,time=time.horizon)$surv
disc.AUC.tab.5[study.num,"seS2"]<-summary(fit.os2,time=time.horizon)$std.err
AUC.tab.5[study.num,"PFS2"]<-my.AUC(data.pfs2,rmean=5)[1]
AUC.tab.5[study.num,"sePFS2"]<-my.AUC(data.pfs2,rmean=5)[2]
AUC.tab.5[study.num,"OS2"]<-my.AUC(data.os2,rmean=5)[1]
AUC.tab.5[study.num,"seOS2"]<-my.AUC(data.os2,rmean=5)[2]
disc.AUC.tab.5[study.num,"PFS2"]<-sum(my.disc.AUC(data.pfs2,max.time=5,disc.fac=1/1.035)[2,6:10])
disc.AUC.tab.5[study.num,"OS2"]<-sum(my.disc.AUC(data.os2,max.time=5,disc.fac=1/1.035)[2,6:10])
#Save a copy of results from each bootstrapped sample
write.csv(boot.auc.pfs2,"filename pfs treat 2.csv")
write.csv(boot.auc.os2,"filename os treat 2.csv")
WinBUGS code for NMA of area under the Kaplan Meier curves and Probability of Surviving up to 5 years – Fixed effect model. Notes: WinBUGS files, including data and initial values are available upon request. Same code may be used for 4-year and discounted AUC data
model{
#Code for 5-year Survival
for (i in 1:ns){
mu.S[i]~dnorm(0,.0001)
for (k in 1:na[i]){
prec.S[i,k]<-pow(se.S[i,k],-2)
y.S[i,k]~dnorm(pi[i,k],prec.S[i,k])
dev.S[i,k]<-(y.S[i,k]-pi[i,k])*(y.S[i,k]-pi[i,k])*prec.S[i,k]
logit(pi[i,k])<-mu.S[i] + delta.S[i,k]
delta.S[i,k]<- d.S[t[i,k]] - d.S[t[i,1]]
}
resdev.S[i] <- sum(dev.S[i,1:na[i]])
}
totresdev.S<-sum(resdev.S[])
#Code for 5-year AUCs (Bivariate for PFS and OS)
for (i in 1:ns){
mu.PFS[i]~dnorm(0,.0001)
mu.PPS[i]~dnorm(0,.0001)
for (k in 1:na[i]){
#Set precision matrix
Sigma[i,k,1,1]<-pow(se.PFS[i,k],2)
Sigma[i,k,2,2]<-pow(se.OS[i,k],2)
Sigma[i,k,1,2]<-corr[i,k]*se.PFS[i,k]*se.OS[i,k]
Sigma[i,k,2,1]<-Sigma[i,k,1,2]
Prec[i,k,1:2,1:2]<-inverse(Sigma[i,k,1:2,1:2])
y[i,k,1:2]~dmnorm(theta[i,k,1:2],Prec[i,k,1:2,1:2])
for (j in 1:2){
diff[i,k,j]<- y[i,k,j]-theta[i,k,j]
z[i,k,j]<- inprod2(Prec[i,k,j,1:2],diff[i,k,1:2])
}
dev[i,k]<-inprod2(diff[i,k,1:2],z[i,k,1:2])
theta[i,k,1]<- mu.PFS[i] + delta.PFS[i,k]
theta[i,k,2]<- theta[i,k,1] + phi[i,k]
phi[i,k]<- mu.PPS[i] + delta.PPS[i,k]
delta.PFS[i,k]<- d.PFS[t[i,k]] - d.PFS[t[i,1]]
delta.PPS[i,k]<- d.PPS[t[i,k]] - d.PPS[t[i,1]]
}
resdev[i] <- sum(dev[i,1:na[i]])
}
totresdev<-sum(resdev[])
#Chemoradiotherapy (treatment code 1) is reference
d.S[1]<-0
d.PFS[1]<-0
d.PPS[1]<-0
for (k in 2:nt){
d.S[k]~dnorm(0,.0001)
d.PFS[k]~dnorm(0,.0001)
d.PPS[k]~dnorm(0,.0001)
}
#Assumed log odds of survival, mean PPS and PFS time over 5-years on reference treatment 1 in UK
m.S<-mu.S[5]
m.PFS<-mu.PFS[5]
m.PPS<-mu.PPS[5]
#Predicted probability of survival and mean survival times in UK population for each treatment
for (k in 1:nt){
#Up to 5 years
logit(S5[k])<- m.S + d.S[k]
meanPFS5[k]<- m.PFS + d.PFS[k]
meanPPS5[k]<- m.PPS + d.PPS[k]
meanOS5[k]<-meanPFS5[k]+meanPPS5[k]
#Long-term
meanPFS[k]<- meanPFS5[k] + S5[k]*C
meanPPS[k]<- meanPPS5[k]
meanOS[k]<-meanPFS[k]+meanPPS[k]
}
#Overall Survival at 5 Years, OR of Survival, Overall Survival relative to CR
for (k in 1:nt){
d.OS5[k]<-d.PFS[k]+d.PPS[k]
OR.S[k]<-exp(d.S[k])
d.OS[k]<-(meanPFS[k]-meanPFS[1])+(meanPPS[k]-meanPPS[1])
}
#Rank treatments
for (k in 1:nt) {
# PFS
rk.PFS[k] <- nt+1-rank(d.PFS[],k)
best.PFS[k] <- equals(rk.PFS[k],1) # Largest is best (i.e. rank 1)
# PPS
rk.PPS[k] <- nt+1-rank(d.PPS[],k)
best.PPS[k] <- equals(rk.PPS[k],1) # Largest is best (i.e. rank 1)
# OS at 5 years
rk.OS5[k] <- nt+1-rank(d.OS5[],k)
best.OS5[k] <- equals(rk.OS5[k],1) # Largest is best (i.e. rank 1)
# OR of Survival
rk.OR.S[k] <- nt+1-rank(OR.S[],k)
best.OR.S[k] <- equals(rk.OR.S[k],1) # Largest is best (i.e. rank 1)
# OS
rk.OS[k] <- nt+1-rank(d.OS[],k)
best.OS[k] <- equals(rk.OS[k],1) # Largest is best (i.e. rank 1)
}
}
WinBUGS code for NMA of area under the Kaplan Meier curves and Probability of Surviving up to 5 years – Random effects model. Notes: WinBUGS files, including data and initial values are available upon request. Same code may be used for 4-year and discounted AUC data
model{
#Code for 5-year Survival
for (i in 1:ns){
delta.S[i,1]<-0
mu.S[i]~dnorm(0,.0001)
for (k in 1:na[i]){
prec.S[i,k]<-pow(se.S[i,k],-2)
y.S[i,k]~dnorm(pi[i,k],prec.S[i,k])
dev.S[i,k]<-(y.S[i,k]-pi[i,k])*(y.S[i,k]-pi[i,k])*prec.S[i,k]
logit(pi[i,k])<-mu.S[i] + delta.S[i,k]
}
resdev.S[i] <- sum(dev.S[i,1:na[i]])
md.S[i,2] <- d.S[t[i,2]] - d.S[t[i,1]]
delta.S[i,2] ~ dnorm(md.S[i,2],tau.S)
}
totresdev.S<-sum(resdev.S[])
#Code for 5-year AUCs (Bivariate for PFS and OS)
for (i in 1:ns){
delta.PFS[i,1]<-0
delta.PPS[i,1]<-0
mu.PFS[i]~dnorm(0,.0001)
mu.PPS[i]~dnorm(0,.0001)
for (k in 1:na[i]){
#Set precision matrix
Sigma[i,k,1,1]<-pow(se.PFS[i,k],2)
Sigma[i,k,2,2]<-pow(se.OS[i,k],2)
Sigma[i,k,1,2]<-corr[i,k]*se.PFS[i,k]*se.OS[i,k]
Sigma[i,k,2,1]<-Sigma[i,k,1,2]
Prec[i,k,1:2,1:2]<-inverse(Sigma[i,k,1:2,1:2])
y[i,k,1:2]~dmnorm(theta[i,k,1:2],Prec[i,k,1:2,1:2])
for (j in 1:2){
diff[i,k,j]<- y[i,k,j]-theta[i,k,j]
z[i,k,j]<- inprod2(Prec[i,k,j,1:2],diff[i,k,1:2])
}
dev[i,k]<-inprod2(diff[i,k,1:2],z[i,k,1:2])
theta[i,k,1]<- mu.PFS[i] + delta.PFS[i,k]
theta[i,k,2]<- theta[i,k,1] + phi[i,k]
phi[i,k]<- mu.PPS[i] + delta.PPS[i,k]
}
md.PFS[i,2] <- d.PFS[t[i,2]] - d.PFS[t[i,1]]
md.PPS[i,2] <- d.PPS[t[i,2]] - d.PPS[t[i,1]]
delta.PFS[i,2] ~ dnorm(md.PFS[i,2], tau.PFS)
delta.PPS[i,2] ~ dnorm(md.PPS[i,2], tau.PPS)
resdev[i] <- sum(dev[i,1:na[i]])
}
totresdev<-sum(resdev[])
#Chemoradiotherapy (treatment code 1) is reference
d.S[1]<-0
d.PFS[1]<-0
d.PPS[1]<-0
#Priors on between-study SDs
sd.S ~ dunif(0,5)
sd.PFS ~ dunif(0,5)
sd.PPS ~ dunif(0,5)
tau.S <- pow(sd.S, -2)
tau.PFS <- pow(sd.PFS, -2)
tau.PPS <- pow(sd.PPS, -2)
for (k in 2:nt){
d.S[k]~dnorm(0,.0001)
d.PFS[k]~dnorm(0,.0001)
d.PPS[k]~dnorm(0,.0001)
}
#Assumed log odds of survival, mean PPS and PFS time over 5-years on reference treatment 1 in UK
m.S<-mu.S[5]
m.PFS<-mu.PFS[5]
m.PPS<-mu.PPS[5]
#Predicted probability of survival and mean survival times in UK population for each treatment
for (k in 1:nt){
#Up to 5 years
logit(S5[k])<- m.S + d.S[k]
meanPFS5[k]<- m.PFS + d.PFS[k]
meanPPS5[k]<- m.PPS + d.PPS[k]
meanOS5[k]<-meanPFS5[k]+meanPPS5[k]
#Long-term
meanPFS[k]<- meanPFS5[k] + S5[k]*C
meanPPS[k]<- meanPPS5[k]
meanOS[k]<-meanPFS[k]+meanPPS[k]
}
#Overall Survival at 5 Years, OR of Survival, Overall Survival relative to CR
for (k in 1:nt){
d.OS5[k]<-d.PFS[k]+d.PPS[k]
OR.S[k]<-exp(d.S[k])
d.OS[k]<-(meanPFS[k]-meanPFS[1])+(meanPPS[k]-meanPPS[1])
}
# Rank treatments
for (k in 1:nt) {
# PFS
rk.PFS[k] <- nt+1-rank(d.PFS[],k)
best.PFS[k] <- equals(rk.PFS[k],1) # Largest is best (i.e. rank 1)
# PPS
rk.PPS[k] <- nt+1-rank(d.PPS[],k)
best.PPS[k] <- equals(rk.PPS[k],1) # Largest is best (i.e. rank 1)
# OS at 5 years
rk.OS5[k] <- nt+1-rank(d.OS5[],k)
best.OS5[k] <- equals(rk.OS5[k],1) # Largest is best (i.e. rank 1)
# OR of Survival
rk.OR.S[k] <- nt+1-rank(OR.S[],k)
best.OR.S[k] <- equals(rk.OR.S[k],1) # Largest is best (i.e. rank 1)
# OS
rk.OS[k] <- nt+1-rank(d.OS[],k)
best.OS[k] <- equals(rk.OS[k],1) # Largest is best (i.e. rank 1)
# QALY
}
}
WinBUGS code to estimate proportion of events occurring each year up to 5 years. Notes: WinBUGS files, including data and initial values are available upon request
model{
for (i in 1:ns){
for (k in 1:na[i]){
for (s in 1:5){
#Likelihood for Survival at times s=1,2,3,4,5
prec.S[i,k,s]<-pow(se.S[i,k,s],-2)
y.S[i,k,s]~dnorm(pi[i,k,s],prec.S[i,k,s])
dev.S[i,k,s]<-(y.S[i,k,s]-pi[i,k,s])*(y.S[i,k,s]-pi[i,k,s])*prec.S[i,k,s]
}
#Model for Survival probs, pi, as a function of the proportion of events in each 1-year time period, rho, by treatment
pi[i,k,5]~dbeta(1,1)
pi[i,k,4]<- pi[i,k,5] + rho[5]*(1-pi[i,k,5])
pi[i,k,3]<- pi[i,k,5] + sum(rho[4:5])*(1-pi[i,k,5])
pi[i,k,2]<- pi[i,k,5] + sum(rho[3:5])*(1-pi[i,k,5])
pi[i,k,1]<- pi[i,k,5] + sum(rho[2:5])*(1-pi[i,k,5])
}
resdev.S[i] <- sum(dev.S[i,1:na[i], 1:5])
}
totresdev<- sum(resdev.S[])
#Dirichlet prior (using Gamma formulation)
for (s in 1:5){
x[s]~dgamma(alpha0[s],1)
rho[s]<- alpha[s]/sum(alpha[1:5])
alpha0[s]<- max(alpha[s],0.1)
log(alpha[s])<- beta[s]
beta[s]~dnorm(0,.01)
}
dum<-t[1,1]
}
WinBUGS code to estimate proportion of events occurring each year up to 4 years. Notes: WinBUGS files, including data and initial values are available upon request
model{
for (i in 1:ns){
for (k in 1:na[i]){
for (s in 1:4){
#Likelihood for Survival at times s=1,2,3,4
prec.S[i,k,s]<-pow(se.S[i,k,s],-2)
y.S[i,k,s]~dnorm(pi[i,k,s],prec.S[i,k,s])
dev.S[i,k,s]<-(y.S[i,k,s]-pi[i,k,s])*(y.S[i,k,s]-pi[i,k,s])*prec.S[i,k,s]
}
#Model for Survival probs, pi, as a function of the proportion of events in each 1-year time period, rho, by treatment
pi[i,k,4]~dbeta(1,1)
pi[i,k,3]<- pi[i,k,4] + rho[4]*(1-pi[i,k,4])
pi[i,k,2]<- pi[i,k,4] + sum(rho[3:4])*(1-pi[i,k,4])
pi[i,k,1]<- pi[i,k,4] + sum(rho[2:4])*(1-pi[i,k,4])
}
resdev.S[i] <- sum(dev.S[i,1:na[i], 1:4])
}
totresdev<- sum(resdev.S[])
#Dirichlet prior (using Gamma formulation)
for (s in 1:4){
x[s]~dgamma(alpha0[s],1)
rho[s]<- alpha[s]/sum(alpha[1:4])
alpha0[s]<- max(alpha[s],0.1)
log(alpha[s])<- beta[s]
beta[s]~dnorm(0,.01)
}
dum<-t[1,1]
}
WinBUGS code to estimate proportion of progressions that are deaths. Fixed effects model. Notes: WinBUGS files, including data and initial values are available upon request
model{ # *** PROGRAM STARTS
for(i in 1:ns){ # LOOP THROUGH STUDIES
mu[i] ~ dnorm(0,.0001) # vague priors for all trial baselines
for (k in 1:na[i]) { # LOOP THROUGH ARMS 62
r[i,k] ~ dbin(p[i,k],n[i,k]) # binomial likelihood
logit(p[i,k]) <- mu[i] + d[t[i,k]] - d[t[i,1]] # model for linear predictor
rhat[i,k] <- p[i,k] * n[i,k] # expected value of the numerators
dev[i,k] <- 2 * (r[i,k] * (log(r[i,k])-log(rhat[i,k])) #Deviance contribution
+ (n[i,k]-r[i,k]) * (log(n[i,k]-r[i,k]) - log(n[i,k]-rhat[i,k])))
}
resdev[i] <- sum(dev[i,1:na[i]]) # summed residual deviance contribution for this trial
}
totresdev <- sum(resdev[]) #Total Residual Deviance
d[1]<-0 # treatment effect is zero for reference treatment
for (k in 2:nt){ d[k] ~ dnorm(0,.0001) } # vague priors for treatment effects
for (l in 1:nt) { pbest[l]<-equals(rank(d[],l),5) }
for (z in 1:(nt-1))
{
caterpillar[z] <- exp(d[z+1])-d[1]
}
# pairwise ORs and LORs for all possible pair-wise comparisons, if nt>2
for (c in 1:(nt-1)) {
for (k in (c+1):nt) {
or[c,k] <- exp(d[k] - d[c])
lor[c,k] <- (d[k]-d[c])
}
}}
WinBUGS code to estimate proportion of progressions that are deaths. Random effects model. Notes: WinBUGS files, including data and initial values are available upon request
# Binomial likelihood, logit link
# Random effects model for multi-arm trials
# based on
# Dias, S., Welton, N.J., Sutton, A.J. & Ades, A.E.
# NICE DSU Technical Support Document 2: A Generalised Linear Modelling Framework
# for Pairwise and Network Meta-Analysis of Randomised Controlled Trials. 2011.
# http://www.nicedsu.org.uk
model {
for(i in 1:NumStudies) { # indexes studies
mu[i] ~ dnorm(0, .0001) # vague priors for all trial baselines
delta[i,1] <- 0 # effect is zero for control arm
w[i,1] <- 0 # multi-arm adjustment = zero for ctrl
for (j in 1:NumArms[i]) { # indexes arms
k[i,j] ~ dbin(p[i,j],N[i,j]) # binomial likelihood
logit(p[i,j]) <- mu[i] + delta[i,j] # model for linear predictor
rhat[i,j] <- p[i,j] * N[i,j] # expected value of the numerators
dev[i,j] <- 2 * (k[i,j] * (log(k[i,j])-log(rhat[i,j]))
+ (N[i,j]-k[i,j]) * (log(N[i,j]-k[i,j]) - log(N[i,j]-rhat[i,j])))
# deviance contribution
# dummy[i,j] <- ArmNo[i,j] # data not used in this model
} # close arm loop
for (j in 2:NumArms[i]) { # indexes arms
delta[i,j] ~ dnorm(md[i,j],taud[i,j]) # trial-specific LOR distributions
md[i,j] <- d[Rx[i,j]] - d[Rx[i,1]] + sw[i,j] # mean of LOR distributions (with multi-arm trial correction)
taud[i,j] <- tau *2*(j-1)/j # precision of LOR distributions (with multi-arm trial correction)
w[i,j] <- (delta[i,j] - d[Rx[i,j]] + d[Rx[i,1]])
# adjustment for multi-arm RCTs
sw[i,j] <- sum(w[i,1:j-1])/(j-1) # cumulative adjustment for multi-arm trials
}
resdev[i] <- sum(dev[i,1:NumArms[i]]) # summed deviance contribution
# dummy2[i] <- Yrs[i] * RefID[i] # data not used in this model
} # close study loop
totresdev <- sum(resdev[]) # total residual deviance
d[1]<-0 # effect is 0 for reference treatment
for (j in 2:NumRx) { # indexes treatments
d[j] ~ dnorm(0, .0001) # vague priors for treatment effects
} # close treatment loop
#sdu ~ dunif(RFXpriorParam1, RFXpriorParam2) # uniform between-trial prior
#sdn ~ dnorm(RFXpriorParam1, RFXpriorParam2) # normal between-trial prior
#sdl ~ dlnorm(RFXpriorParam1, RFXpriorParam2) # lognormal between-trial prior
#sd <- sdu * equals(RFXpriorD,1) + sdn * equals(RFXpriorD,2) + sdl * equals(RFXpriorD,3)
# select correct between-trial prior
tau <- pow(sd,-2) # between-trial precision
sd ~ dunif(0,10)
# Provide estimates of treatment effects T[k] on the natural (probability) scale
#AMean ~ dnorm(meanA, precA)
#APred ~ dnorm(predA, predPrecA)
#for (j in 1:NumRx) {
# logit(Tmean[j]) <- AMean + d[j]
#logit(Tpred[j]) <- APred + d[j]
# }
# pairwise ORs and LORs for all possible pair-wise comparisons
for (c in 1:(NumRx-1)) {
for (j in (c+1):NumRx) {
lOR[c,j] <- (d[j]-d[c])
OR[c,j] <- exp(d[j]-d[c])
}
}
# ranking on relative scale
for (j in 1:NumRx) {
rk[j] <- blnHiGood*(NumRx+1-rank(d[],j)) + (1-blnHiGood)*rank(d[],j)
best[j] <- equals(rk[j],1) # probability that treat j is best
for (h in 1:NumRx) {
pRk[h,j] <- equals(rk[j],h) # probability that treat j is hth best
}
}
#dummy3 <- YrsA # not used in this model
}
Appendix K. Cost-Utility Analysis
Background
Stage IIIA-N2 NSCLC is a common presentation but, despite several RCTs investigating different options, the optimal management strategy for potentially operable patients remains controversial. This stage of NSCLC is generally considered to be the most advanced stage of the disease in which patients would normally still receive radical rather than systemic treatment. Patients with stage IIIA-N2 disease commonly receive chemoradiotherapy (CR) and chemotherapy and surgery (CS) but may receive tri-modality therapy with chemoradiotherapy and surgery (CRS). These are the three treatment options examined in this analysis.
Typically, the chemotherapy and/or radiotherapy components will happen before surgery to make the tumour more operable although patients may receive an amount of either following surgery. Surgery for N2 disease is a complex operation with a high reference cost. The committee prioritised this area for de novo modelling because they wanted to see an analysis that combined progression-free survival (PFS), post-progression survival (PPS), overall survival (OS), adverse event data and costs into a single analysis. The systematic review conducted for this guideline found no published economic evaluations in this area.
Methods
Model Structure
The model is divided into short and long term components. The short term model, covering five years, is based on clinical trial data from six of the studies included in the review, which were prioritised for further analyses based on the relevance of their populations and interventions (Albain 2009, Girard 2009, Eberhardt 2015. Pless 2015, Katakami 2012 and van Meerbeeck 2007a). While four years was the longest common follow up time among all six RCTs, we chose five years as the base case because this only meant excluding Girard 2009, which was the smallest and least relevant study. We felt this was a trade-off worth making to make use of more of the available data, while also making certain modelling assumptions discussed later on more likely to be true. Four year data for all parameters that the time period is relevant to were also sourced and used in sensitivity analysis. Patients surviving the short term model enter the long term model, which takes the form of a Partitioned Survival Analysisb.
The primary clinical evidence for the short term model came from the network meta-analyses (NMAs) of RCTs identified in the clinical review for this guideline. A full write-up of the NMAs can be found in Appendix I but a brief discussion is included here.
It is very common for health economic models in lung cancer to divide patients into pre and post-progression health states, assuming some homogeneity of resource use and utility within those states and that transition between the two indicates something significant in terms of treatment. Overall survival at study endpoint is another key measure that is often reported in NSCLC RCTs. In order to obtain the average amount of time a patient undergoing any of the three interventions would spend in the progression free and progressed health states we digitised all the survival curves in the trials the committee prioritised for inclusion in the NMAs via the use of the Guyot et al algorithmc. This algorithm makes use of digitised survival curves (in this case we used Enguaged for this purpose) and the numbers at risk data that are commonly reported underneath Kaplan-Meier plots in RCTs to generate synthetic individual patient data. The algorithm creates a survival time and a censorship or event variable for each “patient” in the trial, which is amenable to the usual survival analysis techniques. Survival analysis on the synthetic data has been found to accurately reproduce the same analysis conducted on the real individual patient data from the trials in a large number of examplesc.
Once the individual patient data had been obtained it was possible to calculate the area under the curve (AUC), which is equivalent to the mean time in state (restricted by the trial endpoint) and its standard error for both PFS and OS. Since PFS and OS are correlated, a correlation coefficient between the two was calculated and used in a bivariate NMA model that produced results for both PFS and OS for each of the three interventions. Since mean PPS would be equal to OS minus PFS for each iteration of the NMA, this statistic was also calculated via simple subtraction. Since the OS and PFS were obtained over five years of trial data, the AUC statistics were adjusted for discounting. A separate NMA model also calculated the probability of survival at study endpoint.
All NMAs were conducted separately on two study endpoints; four and five years post treatment. The four year data were available for all six RCTs but five year data were available for all except the smallest and least relevant RCT so the committee preferred the five year analysis in the base case, with the four year data being used in sensitivity analysis. In either case, the committee instructed us to assume that all, or at least the vast majority, of the ~15% of patients who had survived to five years post treatment were in remission and would continue into the long-term model progression free until death. This assumption may be reasonable, given that the PFS and OS Kaplan-Meier curves reported in the trials showed a strong tendency toward convergence at five years.
For the long term component of the model, a patient registry containing survival data conditional on NSCLC stage IIIA-N2 patients having survived for five years was obtained. Survival curves were fitted to this data and used in a long term Partitioned Survival Analysis with only two health states; (alive and) progression free and dead.
The structure of the model is shown in Figure 13.
Figure 13. Economic Model Structure (time in state up to 5 years is dictated by NMAs)
Model Parameters
Utility Data
No direct health related quality of life data for progression free and post progression survival were available for patients with stage IIIA-N2 NSCLC. However, a targeted search was undertaken and a large number of potentially relevant data sources were identified that related to people with Stage III NSCLC undergoing surgery. Of these, the three studies the committee thought the most relevant are displayed in Table 24. A random effects model was chosen to pool these data because the I-squared statistic equalled 80%, indicating high between study heterogeneity.
No relevant post-progression utility estimates were identified so a generic post-progression adjustment value taken from a study widely used in economic models for advanced NSCLC was used (Nafees 2008). The committee agreed that it was likely patients undergoing surgery would experience some reduction in health related quality of life for about three months while they recovered. This was borne out in the evidence from Bendixen 2016e, a trial that investigated HRQoL in patients having surgery for NSCLC. We used data on EQ-5D measured at various time points in the thoracotomy arm of the trial to calculate the QALY loss from surgery by assuming that any dips below a linear trajectory between the time periods of 0 weeks and 12 weeks were due to surgery. The resulting difference between the areas under the curve for the observed values and the linear trajectory, calculated using simple averaging methods between observed time points, gave a QALY loss due to surgery of −0.012. This value was applied only to people actually undergoing surgery (see the section further down discussing drop-out rates).
For the long term portion of the model, in which people were assumed to remain progression-free until death, the progression-free utility value was multiplied by the age specific decrements that would be expected in the general population (Kind et al 1999). More specifically, the age specific value at each cycle was looked up from a table containing general population utility values and divided by the population level age specific utility value at cycle 0 of the long term model. This figure was then multiplied by the progression free survival utility value to give the utility at future cycles including any appropriate decrements for advanced age. Weighted averages were used for men and women assuming 53.4% of people in the model were men (NCLA 2017 data on general lung cancer presentation). To reflect the population in the underpinning trials, the starting age in the model was 60 (and therefore 65 in the long term model).
Table 25. General Population Utility Estimates for Use in Long Term Multiplier
Adverse events were assumed to be acute in nature and not contribute meaningfully to QALY losses. Since adverse event rates did not differ greatly between the interventions, this limitation was assessed as minor.
Progression Free and Post Progression Survival Time (Short Term Model)
A single bivariate NMA model produced the estimates for discounted PFS and PPS. A brief discussion of this contained in the Model Structure section above and a full write up of this analysis can be found in Appendix I. The NMA had 50,000 burn-in iterations that were then discarded. 10,000 values that had been thinned by 5 were taken from the next 50,000 iterations and used in the economic model. For each run of the model, discounted PFS and PPS values for all three interventions came from a randomly sampled line of this CODA output. The use of a single line of CODA for all data points was essential to preserve the correlation structure in the posterior distributions.
The discounted average pre and post progression survival time were multiplied by the relevant utility values to produce QALYs over 5 years. A surgery specific QALY decrement (see above) was applied to people receiving surgery in the CR and CRS model arms.
Survival at study endpoint
The probability of survival at study endpoint came from the relevant NMA (see Appendix I for a full discussion). The NMA had 50,000 burn-in iterations that were then discarded. 10,000 values that had been thinned by 5 were taken from the next 50,000 iterations and used in the economic model. For each run of the model, probability values for all three interventions came from a randomly sampled line of this CODA output. The use of a single line of CODA for all data points was essential to preserve the correlation structure in the posterior distributions. Patients who survived the short term section of the model proceeded into the long term section.
Table 26. NMA Results - Fixed Effects
Table 27. NMA Results - Random Effects
While the relative effects derived from the NMA are insensitive to the choice of baseline values for chemoradiotherapy for PFS, PPS and probability of survival, the absolute values shown in Table 26 and Table 27 are highly sensitive to this choice. We chose to base this data on van Meerbeeck et al 2007 because it the largest study and because it was not characterised by the limitations of the other chemoradiotherapy studies; Eberhardt 2015 (a partially indirect population) and Albain 2009 (a US healthcare setting). The choice of study is expected to make little difference to the model’s results as they relate to PFS and PPS but this is not true for the probability of survival. The relative effect for this outcome is an odds ratio, which is then multiplied by the odds of surviving into the long term model on chemotherapy. If the odds of surviving are very large or very small (prob = 0% or 100%) then the resulting absolute difference in probabilities, and therefore differential number of patients in the long term model, will be small. If the odds are close to even (prob = 50%), as in the case of the Eberhardt data then the resulting differential will be large. We used data from Eberhardt as a sensitivity analysis.
Adverse Events
The committee indicate that we should assume adverse events were acute in nature and that they would be unlikely to materially affect patients’ health related quality of life for any extended period. The numbers of reported adverse events at grade 4 were extremely low and therefore it was highly uncertain whether they differed meaningfully between interventions. The committee asked us to account for only grade 3+ adverse events in the model as these would be expected to incur a hospital admission and were therefore would potentially influence the net monetary benefit associated with the interventions. Grade 3+ adverse events were treated homogenously in the model (i.e. no difference between grades 3 and 4 and no difference between the clinical nature of events). This approach was taken for several reasons; as mentioned above, grade 4 events were rare, events were reported heterogeneously among trials and the specific nature of events was not expected to affect the net monetary benefit calculations within the model due to lack of meaningful differences in HRQoL loss or costs accrued.
We examined the data and determined that only the larger trials conducted by Pless 2015, Eberhardt 2015 and Albain 2009 had reported adverse events comprehensively enough to give us some confidence in the homogeneity of their data collection and reporting methods. We fitted a baseline incidence rate meta-analysis to the arms containing CRS (as the intervention with the most data and trial arms) where events were the total number of events at grade 3 and above and person years at risk were determined by multiplying the sample size by the total area under the overall survival curve at 5 years (which is equal to restricted mean person years lived for the patients in those trial arms). The test for heterogeneity was significant (p<0.0001) so we preferred to use results from a random effects model for the base case analysis.
We then used the same data on events and person years at risk from both arms of the Pless trial to calculate the incidence rate ratio for CS vs CRS. The incidence rate ratio for CR vs CRS was calculated by pooling the data from the Albain and Eberhardt trials in a meta-analysis with random effects again being preferred due to heterogeneity (p=0.019).
Late on in development we received additional data from the EORTC on adverse events in the van Meerbeeck trial. This enabled us to fit a network meta-analysis for this outcome using the data from all four large trials. We decided that because the adverse events would be expected to occur within a reasonably short time frame (certainly those that were directly attributable to the interventions) we could assume a homogenous follow up time in our analysis. We therefore used the person years at risk as detailed above and selected a poisson likelihood, log link model for the analysis (the WinBUGS code is available in Appendix I). The NMA calculated hazard ratios, which we applied directly to the baseline incidence rate and overall survival AUC to calculate total events. The deviance information criterion for the random effects model was only 2 points lower so we preferred the fixed effects model in the base case. The credible intervals for the random effects model are very wide so introduce significant uncertainty into the model but have been examined in a sensitivity analysis. Of note, we decided to use a multivariate normal distribution to incorporate these data into the probabilistic sensitivity analysis rather than using the CODA outputs from the NMA so as not to slow down the model. We do not expect this to have affected the results.
The committee examined the resulting data and noted that the total number of events for CS and CR remained roughly the same and that they were both higher than CRS The committee were unsure about the clinical plausibility of this, given that CRS is the more intense intervention but they noted that it could be explained to some extent by the finding that more people in the CS strategy actually go on to have surgery. Ultimately they decided to prefer the pairwise approach over the NMA in the base case as it introduced less uncertainty into the probabilistic sensitivity analysis but in interpreting the results were mindful that few significant differences has been observed in the GRADE tables. A sensitivity analysis where event rates were equal was therefore also specified.
For the 4-year sensitivity analysis we calculated the baseline incident rates using the same number of adverse events and the 4-year person years at risk data. We assumed the pairwise incident rate ratios would remain the same. These data were multiplied by the total person years at risk to give total adverse events at 4 years. These were very similar to using the 5-year data. We did not fit a 4-year NMA because the base case analysis was chosen to be pairwise.
Costs of Initial Treatment
The committee examined the dosing regimens in the RCTs and noted that the interventions were delivered quite heterogeneously (varied number of cycles of chemotherapy, grays and fractions of radiotherapy and timing of both interventions). They noted that none of the studies were set in the UK and decided on a set of resource uses that they felt were broadly representative of UK practice as well as being similar to the range observed in the trials. This was four cycles of chemotherapy and 55 grays in 20 fractions for radiotherapy in the base case. There are a large number of possible platinum doublet chemotherapy combinations used in current UK practice, which all cost a similar amount. As costing all these individually and taking a weighted average would not have meaningfully added to the accuracy of the model, we decided to cost a representative treatment. The committee decided that we should use carboplatin and oral vinorelbine for this purpose and supplied us with the typical doses.
Surgery was costed using the NHS reference cost for “Complex Thoracic Procedures, 19 years and over, with CC Score 3-5”. The committee felt this was the most representative cost as the procedure was expected to be more complicated than most lobectomy operations, which were costed at “…CC score 0-2”. A proportion of operations for N2 stage disease are pneumonectomies which the committee also felt would be covered by this reference cost.
| Costs of Interventions | ||
|---|---|---|
| Radiotherapy Costs | ||
| Hypofractionated Radiotherapy 55 Gy/20#/4 weeks | ||
| Define volume for simple radiation therapy with imaging and dosimetry | 1 | Resource use from CG121 |
| Deliver a fraction of complex treatment on a megavoltage machine | 1 | Resource use from CG121 |
| Deliver a fraction of treatment on a megavoltage machine | 19 | Resource use from CG121 |
| Define volume for simple radiation therapy with imaging and dosimetry cost - SC03Z | £362.59 | National Schedule of Reference Cost 2016/17 |
| Deliver a fraction of complex treatment on a megavoltage machine cost - SC23Z | £138.42 | National Schedule of Reference Cost 2016/17 |
| Deliver a fraction of treatment on a megavoltage machine cost - SC22Z | £103.37 | National Schedule of Reference Cost 2016/17 |
| Total cost of Standard Fractionated Radiotherapy 60–66 Gy/30–33#/6–6.5 weeks | £2,465.07 | Calculated |
| Proportion Receiving 55 in 20 | 1 | Committee Assumption |
| Total Radiotherapy Cost | £2,465.07 | Calculated |
| Systemic Anti-Cancer Therapy (platinum doublet chemotherapy) | ||
| Number of cycles | 4 | Committee Assumption |
| Outpatient appointment - SB12Z | £173.99 | National Schedule of Reference Cost 2016/17 |
| Administration appointment (0.25 of band 4 time, at £28ph) | £7.00 | PSSRU 2017 for band 4 hourly cost |
| Vinorelbine | ||
| Resource use per cycle | ||
| 80mg capsule | 2 | Committee Assumption |
| 20mg capsule | 4 | Committee Assumption |
| Cost per unit of resource | ||
| 80mg capsule | £175.50 | NHS Indicative Price (BNF Online) |
| 20mg capsule | £43.98 | NHS Indicative Price (BNF Online) |
| Total cost of Vinorelbine (per cycle) | £526.92 | Calculated |
| Carboplatin | ||
| Resource use per cycle | ||
| Dose of Carboplatin required per cycle (mg) | 575 | Committee Assumption |
| Dose per vial Carboplatin 150mg/15ml solution for infusion vials (mg) | 150 | Committee Assumption |
| Number of Carboplatin 150mg/15ml solution for infusion vials required | 3.83 | Committee Assumption |
| Cost per unit of resource | ||
| Price per vial Carboplatin 150mg/15ml solution for infusion vial | £6.35 | eMIT National 2016/2017 NCP Code DHE001 |
| Total cost of Carboplatin (per cycle) | £24.34 | Calculated |
| Dexamethasone 8mg bd, reducing over 4 weeks, top dose 1 week and taper down | £74.34 | Drug Tarriff 2018 |
| Total cost of SACT (per cycle) | £750.84 | Calculated |
| Total cost of SACT (all cycles) | £3,003.36 | Calculated |
| Surgery - Complex Thoracic Procedures, 19 years and over, with CC Score 3-5 | £ 7,562.42 | National Schedule of Reference Cost 2016/17 |
Progressions (costs and events)
Since progression-free survival represents both patients who have not either progressed to a more advanced stage of disease or died, obtaining the number of progressions that are in fact deaths is necessary. These data were available in Albain 2009 and Pless 2015 and in a personal communication from the EORTC, who hold the data for van Meerbeeck 2007. The data from Pless and van Meerbeeck was pooled in a fixed effects meta-analysis (heterogeneity p=0.18) to obtain the proportion of progressions that were deaths for the CS intervention, the log-odds ratios were then analysed in NMA (see Appendix J for details) and applied to the pooled CS estimate to calculate the proportions for CR and CRS. These data were assessed as having good face validity as it would be reasonable to expect the surgical intervention arms to include more early deaths due to the invasive nature of the interventions. These parameters were only important for costs in the economic model, however, as all survival data of interest had already been taken into account via the other NMAs..
Upon progressions that were not deaths, patients were assumed to be treated with another round of systemic therapy. We had no data on the specific types of progression and it was not clear that progression type or the indicated treatment would be expected to differ significantly between the interventions so the committee thought this simplifying assumption reasonable. There are a very large number of systemic therapy options available in NSCLC (see RQ 3.3 of this update for a full algorithm) so costing them all and factoring in their differential benefits in this patient population would have been impractical and subject to high uncertainty. These treatment options have typically been the subject of NICE Technology Appraisals and therefore represent cost-effective additions to the care pathway, but additions that the committee was aware were unlikely to add much in terms of net monetary benefit. This is because Technology Appraisal approved drugs in advanced cancer rarely have base case ICERs significantly lower than the upper limit of the ICER range normally considered cost effective by NICE. The committee also noted that much of the evidence in this model came from survival data collected before many of these drugs were widely available. They therefore thought that the net monetary benefit associated with systemic therapy could reasonably be approximated using the costs of platinum doublet chemotherapy. Four cycles of oral vinorelbine with carboplatin was again chosen for this purpose and the overall cost of systemic therapy for progression was explored in sensitivity analysis.
Table 29. Progressions that are deaths
The committee noted the convergence of the overall and progression free survival curves and made the assumption that progression-free survival would equal overall survival at the study endpoint of 5 years. They felt that NSCLC would be highly unlikely to recur in the vast majority of patients who were alive and unprogressed at this point. The number of progressions for each intervention during the first 5 years was therefore calculated by multiplying one minus the proportion still alive by one minus the proportion of progressions that were deaths.
The total number of deaths was equal to one minus the probability of survival at study endpoint and a cost of death representing a total package of end-of-life care was applied that was drawn from a study including the costs accrued by cancer patients in their last 90 days of life (Georghiou and Bardsley 2014k). This data source had also been used by NICE’s recently published guideline on Early and Locally Advanced Breast Cancer. The cost of existing in the pre and post progression states for 90 days, weighted by the proportion of people who were expected to die directly from each state was then subtracted to give the total death-attributable cost. We assigned the overall value an arbitrary high standard error equal to a quarter of the mean as these data were quite uncertain.
Discounting
Discounting was implemented at 3.5% throughout the model. While the NMAs already discussed provided discounted values for PFS and PPS and probability of OS, which could be multiplied directly by state membership and utility estimates to produce appropriate discounted values, another solution was needed for event costs. Another two NMAs were therefore conducted (see full discussion in Appendix I) that calculated the proportion of progressions and deaths that occurred in each year. These proportions were multiplied by the total number of deaths and progression events and the appropriate discount factor for each year of the model to give a total weighted discounted average cost for both types of events.
Drop Out Rates
The overall and progression-free survival curves provided intention-to-treat effectiveness data for each arm of each study. Not all patients in the surgery arms actually had surgery, however, through either dying, not being fit enough or changing their mind by the end of chemoradiotherapy. The committee therefore thought that the cost of the strategies including surgery should reflect these data. We were able to obtain the proportion of people actually undergoing surgery from the CS and CRS arms of all the trials. We pooled the data for proportion of patients undergoing surgery and used a random effects model due to high statistical heterogeneity. Because the smaller studies were less certain and contributed quite a lot of heterogeneity to this calculation we excluded them and pooled only the large studies in a fixed effects meta-analysis. We repeated this same procedure for CS; both the meta-analyses with and without large trials were fitted using random effects models to account for statistical heterogeneity. In the base case, we used the data containing only large trials because we thought it more reliable but the value obtained using all the trials and a value of 100% were examined in sensitivity analysis.
Health State Costs
No background healthcare resource use data was available for patients with NSCLC stage IIIA-N2. We examined the literature for inspiration and presented a number of possible resource uses to the committee. The committee debated these data and, incorporating their own clinical experience, settled on the assumptions in Table 33 and Table 34 as being broadly representative of a typical patient in the progression free and progressed states. The total monthly average cost is the sum of the product of % of patients, units and costs for each type of resource.
Table 33. Monthly Progression Free State Costs
Table 34. Monthly Progressed State Costs
To calculate total costs for the short term model these costs were multiplied by the average discounted time that patients spent in each state, which was derived from the relevant NMA.
Long Term Model
Patients surviving the short term model entered the long term model, which was a partitioned survival model with two states; dead and alive + progression free. It was assumed that no progressions took place among the surviving patients and they had, to all intents and purposes been cured of their lung cancer. Death events were accrued at a rate equivalent to the difference in the death state membership from cycle to cycle. The long term model was run on a monthly cycle length and a half-cycle correction using the life table method was applied. As discussed earlier, progression-free utility estimates were adjusted to reflect the decline in HRQoL in the general population at older ages. Progression-free costs continued to be applied in the model but at a rate of only 20% to reflect the assumptions that patients would be permanently remitted after 5 years but the committee felt patients would still continue to interact with services to some degree, especially if they had impaired lung function following radical treatment.
In order to obtain appropriate survival curves we interrogated the SEER registryl, which was chosen because it was the only registry we knew about with the ability to extract the data we needed. The database was queried for survival data for patients who were diagnosed between 1988-2003, aged 35-79, had stage IIIA-N2 lung cancer upon diagnosis and had survived five years after their initial diagnosis. We fit survival curves to the data and selected the two with the lowest AIC statistics for use within the model as the base case and in sensitivity analysis. These were Weibull and exponential curves fitted to data from 2,865 patients. From Figure 14, it can be seen that they fitted the survival data well. The AUC (or mean survival time) for these curves was about seven years. The data were somewhat out of date and we were unable to identify any data that would enable us to differentiate these curves by initial treatment but the committee thought that as they were meant to represent a cured population, these limitations were minor. The same process as this was undertaken to parameterise the 4-year sensitivity analysis, with Weibull and Exponential curves again providing the best fit to the data (N=3,703).
Sensitivity Analysis
Sensitivity and scenario analyses was conducted by altering key parameters or groups of parameters including changing the short term element of the model to cover four years instead of five, using random effects NMAs instead of fixed effects, changing key cost and utility parameters, setting probability of survival at study endpoints and various other uncertain data equal among interventions, using different survival curves and altering the discount rate.
Probabilistic sensitivity analysis was performed by assigning parameters with appropriate probability distributions that reflected our uncertainty about their mean values. Of note, the NMAs used the relevant CODA. The very bottom end of the posterior distributions for AUC values for PFS and PFS in the random effects models had to be truncated at 0. This was because the NMA input and output data were on the natural scale (i.e. number of years) and so some impossible negative AUC values arose due to the wide credible intervals in the posterior distribution of the random effects models. This was only a small amount of data so was noted as a minor limitation for the PSA in the random effects scenario analysis.
Particularly uncertain costs that were heavily influenced by assumptions (such as the state membership costs and the cost of death) were arbitrarily assigned a high standard error equal to the mean divided by four. As noted in the adverse events section, the hazard ratios derived from NMAs were parameterised using a multivariate normal distribution on the log scale to reduce model size and running time.
Results
All base case results presented in this section are the mean of 5,000 probabilistic iterations of the model unless otherwise stated. The base case assumptions were; 5 year fixed effects NMA data, random effects pairwise adverse event data.
Table 36. Base Case Results (Fixed Effects NMAs)
Table 37. Base Case Results (Random Effects NMAs)
Figure 15. Cost Effectiveness Plane CRS vs CR (base case, fixed effects NMAs)
Figure 16. Cost-Effectiveness Acceptability Curve (base case, fixed effects NMA)
Figure 17. Cost-Effectiveness Plane CRS vs CR (random effects NMAs for PFS, PPS and Prob S)
Figure 18. CEAC (random effects NMAs)
Table 38. Pairwise ICERs from Scenario Analyses (results are deterministic unless otherwise noted)
Discussion
CS produced QALY and life year gains of 0.04 and 0.055 over CR, whereas CRS produced QALY and life year gains of 0.21 and 0.23 over CR. The model results show a high probability that that CRS produces the most life years and QALYs. The probability that CRS generates more QALYs than CR is 94% in the base case analysis and 83% if random effects NMAs are used. There were no plausible and robust sensitivity analyses in which CS would be considered cost-effective compared to CR at £20,000 per QALY gained and the comparison of CRS vs CS uniformly produced ICERs of less than £20,000/QALY. CS produced more QALYs than CR in 60% of model iterations and CRS produced more QALYs than CS in 85%. The model provides evidence that CS is unlikely to be a cost-effective option, being extendedly dominated by the combination of CR and CRS and having a high ICER vs CR, which is subject to high uncertainty. The cost effectiveness acceptability curve always showed CS as having a relatively low probability of being the most cost-effective option, regardless of the value of a QALY.
The model was quite insensitive to a large number of the parameters examined in sensitivity analysis and consistently produced ICERs for CRS vs CR of around or below £20,000/QALY. One particularly noteworthy source of uncertainty was the sensitivity analysis around the probability of survival at study endpoint, which produced an ICER over £30,000/QALY for CRS vs CR. The fixed effects NMA for this outcome did not find any significant differences among interventions for this outcome although 86% of the probability mass for the difference in this outcome favoured CRS over CR. In the analysis where the probability of survival at study endpoint is set equal, CRS still produces more QALYs than CR in 89% of model iterations.
The mean ICERs were very similar using random rather than fixed effects NMAs. While these models were not found to be statistically preferable, they might have been more appropriate given some of the heterogeneity in patient populations and interventions in the included studies. The cost-effectiveness plane shows a very wide dispersion of results for the random effects analysis.
CS was always extendedly dominated by the combination of CR and CRS in the scenario analyses. Furthermore, in the majority of these scenario analyses, the ICER for CS vs CR was above £30,000/QALY and was highly sensitive to a number of parameters. This variability in ICERs is due to the small QALY improvement of CS over CR.
Of note, if the Eberhardt data are used as the baseline for PFS, PPS and the probability of survival, the ICERs for the surgical options are much lower. This is because the odds ratio for survival derived from the NMA is applied to a much larger baseline odds of a survival, which produces a greater differential probability of surviving into the long term model. Overall survival in the Eberhardt trial was close to three times that in the van Meerbeeck trial at five years. The choice of trial for the base case analysis is discussed in the methods section but it is likely that the ‘true’ ICERs for the surgical options lie somewhere between the base case and the Eberhardt data i.e. they are likely more cost-effective than our base case results suggest.
Overall, the results of our model suggest that CRS is likely to be a cost-effective improvement over CR but that CS is unlikely to be, albeit with some uncertainty in the underpinning clinical data. This is due largely to the results of the NMAs conducted for this guideline showing that people receiving CRS spend significantly longer progression free and are potentially more likely to be cured of their lung cancer. Differences in adverse events between the different interventions were small and somewhat uncertain and had a fairly significant effect on the results for CS. Adverse event data did not affect the ICER for CRS vs CR when the rates were set equal. The ICER for CRS vs CR was affected somewhat by the assumption that not all patients would actually continue on to surgery after completing chemoradiotherapy but remained under £30,000 per QALY when this assumption was relaxed. The ICERs were also sensitive to the cost of surgery and the costs of progressed state membership although again remained around or under £30,000/QALY for CRS vs CR when extreme assumptions were tested.
Strengths and Limitations
Our analysis has a number of important strengths. As far as we are aware is the first cost-effectiveness analysis examining treatment options in people with NSCLC stage IIIA-N2, which is a common presentation that is managed variably across the UK NHS and the world. It is based on novel and high quality methods for synthesising the wealth of data available in the trials conducted to date. In terms of its conclusions for UK practice, the model is insensitive to the vast majority of sensitivity and scenario analyses that were conducted to explore the limitations and uncertainties in the underlying data.
The model also has a number of limitations of varying importance. NSCLC stage IIIA-N2 is a heterogeneous condition and we were unable to find sufficient evidence that enabled us to examine the relative cost-effectiveness of treatment options in different subgroups, for example those indicated for lobectomy versus pneumonectomy, bulky versus non-bulky and multiple versus single-station N2. The model used PFS utility estimates drawn from a potentially clinically and somewhat culturally indirect population, a progression utility adjustment from an indirect population as well as making several strong assumptions about costs and resource use associated with state membership and death events. We were unable to account for advances made in systemic treatment (for example targeted and immunotherapy) although given that these new drugs are usually very expensive, we speculate that surgical options might be more cost-effective because they are associated with a lower probability of disease progression than CR. Most of the data used to drive the model was collected before these drugs were widely available but it is unclear how much survival time, if any, could be attributable to them being used in patients with more advanced disease. Furthermore, people who progress often receive multiple lines of systemic treatment, which was not accounted for at all in our model. Again though, this could make surgical options more cost-effective because more progressions occur in CR and more time is spent in the post-progression state. Adverse events were modelled quite crudely but made little difference to the conclusions. The background resource use of patients surviving into the long term model was uncertain and had a big effect on ICERs. The NMAs driving the model in the base case were fixed effects models with the two statistically significant findings that CRS provided more progression free life years than CR and that CR provided more post-progression life years. While not preferable on grounds of statistical model fit, it might have been more appropriate to use the random effects data, which did not find any statistically significant outcomes (although point estimates remained roughly consistent). The results of the model when driven by the random effects data are more uncertain although the base case ICERs are similar. The model also did not specifically include a strategy of CR followed by immunotherapy as this is currently not a routine option for people with NSCLC stage IIIA-N2 on the UK NHS. The committee were aware of the existence of relevant data from the PACIFICm trial but the NICE Technology Appraisal on durvalumab, the immunotherapy used in that trial, is not expected to publish until after the publication of this guideline. While that trial was not conducted in a resectable stage IIIA-N2 population and is therefore not directly applicable to this review question, its evidence hints that there may be another option in this decision space in the future.
Appendix L. Research recommendations
|
|
|---|---|
| Population | Patients with NSCLC stage IIIA-N2 who have received multimodality treatment (including surgery) |
| Characteristics of interest | Overall survival Health-related quality of life Adverse events grade 3 or above Safety |
| Study design | Randomised controlled trial |
|
|
|---|---|
| Importance to patients, service users or the population | Immunotherapy has been shown to be effective in a variety of NSCLC indications but there is currently no evidence on whether it is clinically or cost effective for people with stage IIIA-N2 non-small-cell lung cancer following surgery. There is also no evidence on whether it could be used as a replacement or adjunct to current multimodality treatment. The committee made a research recommendation to address this. |
| Relevance to NICE guidance | Medium priority: a recommendation was made for people with stage III a – N2 who are well enough for multimodality therapy and who can have surgery, to consider chemoradiotherapy with surgery. This updated recommendation could lead to a change in current practice in that more tri-modality therapy might be performed. The role of immunotherapy in current multimodality treatment is worthy of further research to potentially strengthen this recommendation and provide further treatment options for this presentation where survival is currently poor. |
| Current evidence base | The updated recommendation is based on statistical and health economic analysis, therefore more RCT studies are required in a UK setting. |
| Equality | This study could improve equality of access to multimodality treatment for stage IIIa-N2 disease and ensure more people receive this potentially curative treatment. |
| Feasibility | There is a large enough population of people with this condition and the interventions are available in current clinical practice. |
Footnotes
- a
Please see the section on ‘Clinical Studies – Included’ above for full references
- b
NICE DSU TSD 19: Partitioned survival analysis for decision modelling in health care: a critical review (2007)
- c
Guyot et al (2012) Enhanced secondary analysis of survival data: reconstructing the data from published Kaplan-Meier survival curves. BMC Medical Research Methodology [PMC free article: PMC3313891] [PubMed: 22297116]
- d
- e
Bendixen et al (2016) Postoperative pain and quality of life after lobectomy via video-assisted thoracoscopic surgery or anterolateral thoracotomy for early stage lung cancer: a randomised controlled trial. Lancet Oncology [PubMed: 27160473]
- f
Grutters et al (2010) Health-related quality of life in patients surviving non-small cell lung cancer. Thorax [PubMed: 20861294]
- g
Tramontano et al (2015) Catalog and Comparison of Societal Preferences (Utilities) for Lung Cancer Health States: Results from the Cancer Care Outcomes Research and Surveillance (CanCORS) Study. Medical Decision Making [PMC free article: PMC8513729] [PubMed: 25670839]
- h
Yang et al (2014) Estimation of loss of quality-adjusted life expectancy (QALE) for patients with operable versus inoperable lung cancer: Adjusting quality-of-life and lead-time bias for utility. Lung Cancer [PubMed: 25178685]
- i
Nafees et al (2008) Health state utilities for non small cell lung cancer. Health and Quality of Life Outcomes [PMC free article: PMC2579282] [PubMed: 18939982]
- j
- k
- l
- m
Antonia et al (2017) Durvalumab after Chemoradiotherapy in Stage III Non–Small-Cell Lung Cancer. New England Journal of Medicine [PubMed: 28885881]
Final
Evidence reviews
These evidence reviews were developed by the NICE Guideline Updates Team
Disclaimer: The recommendations in this guideline represent the view of NICE, arrived at after careful consideration of the evidence available. When exercising their judgement, professionals are expected to take this guideline fully into account, alongside the individual needs, preferences and values of their patients or service users. The recommendations in this guideline are not mandatory and the guideline does not override the responsibility of healthcare professionals to make decisions appropriate to the circumstances of the individual patient, in consultation with the patient and/or their carer or guardian.
Local commissioners and/or providers have a responsibility to enable the guideline to be applied when individual health professionals and their patients or service users wish to use it. They should do so in the context of local and national priorities for funding and developing services, and in light of their duties to have due regard to the need to eliminate unlawful discrimination, to advance equality of opportunity and to reduce health inequalities. Nothing in this guideline should be interpreted in a way that would be inconsistent with compliance with those duties.
NICE guidelines cover health and care in England. Decisions on how they apply in other UK countries are made by ministers in the Welsh Government, Scottish Government, and Northern Ireland Executive. All NICE guidance is subject to regular review and may be updated or withdrawn.
- Evidence reviews for the clinical and cost effectiveness of treatment regimens for the treatment of operable Stage IIIA-N2 NSCLC
- Review protocols
- Methods
- Literature search strategies
- Evidence study selection
- Clinical evidence tables
- GRADE tables
- Meta-analyses
- Excluded Studies
- References
- Network Meta-analysis
- Cost-Utility Analysis
- Research recommendations
- Neoadjuvant treatment followed by surgery versus definitive chemoradiation in stage IIIA-N2 non-small-cell lung cancer: A multi-institutional study by the oncologic group for the study of lung cancer (Spanish Radiation Oncology Society).[Lung Cancer. 2018]Neoadjuvant treatment followed by surgery versus definitive chemoradiation in stage IIIA-N2 non-small-cell lung cancer: A multi-institutional study by the oncologic group for the study of lung cancer (Spanish Radiation Oncology Society).Couñago F, Rodriguez de Dios N, Montemuiño S, Jové-Teixidó J, Martin M, Calvo-Crespo P, López-Mata M, Samper-Ots MP, López-Guerra JL, García-Cañibano T, et al. Lung Cancer. 2018 Apr; 118:119-127. Epub 2018 Feb 14.
- Role of surgery in N2 NSCLC: pros.[Jpn J Clin Oncol. 2016]Role of surgery in N2 NSCLC: pros.Shien K, Toyooka S. Jpn J Clin Oncol. 2016 Dec; 46(12):1168-1173. Epub 2016 Sep 21.
- Review Is There a Survival Benefit in Patients With Stage IIIA (N2) Non-small Cell Lung Cancer Receiving Neoadjuvant Chemotherapy and/or Radiotherapy Prior to Surgical Resection: A Systematic Review and Meta-analysis.[Medicine (Baltimore). 2015]Review Is There a Survival Benefit in Patients With Stage IIIA (N2) Non-small Cell Lung Cancer Receiving Neoadjuvant Chemotherapy and/or Radiotherapy Prior to Surgical Resection: A Systematic Review and Meta-analysis.Xu YP, Li B, Xu XL, Mao WM. Medicine (Baltimore). 2015 Jun; 94(23):e879.
- Long-term survival of stage T4N0-1 and single station IIIA-N2 NSCLC patients treated with definitive chemo-radiotherapy using individualised isotoxic accelerated radiotherapy (INDAR).[Radiother Oncol. 2014]Long-term survival of stage T4N0-1 and single station IIIA-N2 NSCLC patients treated with definitive chemo-radiotherapy using individualised isotoxic accelerated radiotherapy (INDAR).Reymen B, van Baardwijk A, Wanders R, Borger J, Dingemans AM, Bootsma G, Pitz C, Lunde R, Geraedts W, Lambin P, et al. Radiother Oncol. 2014 Mar; 110(3):482-7. Epub 2014 Jan 17.
- Review Current status of induction treatment for N2-Stage III non-small cell lung cancer.[Gen Thorac Cardiovasc Surg. 2014]Review Current status of induction treatment for N2-Stage III non-small cell lung cancer.Yamaguchi M, Sugio K. Gen Thorac Cardiovasc Surg. 2014 Nov; 62(11):651-9. Epub 2014 Jul 18.
- Evidence reviews for the clinical and cost effectiveness of treatment regimen fo...Evidence reviews for the clinical and cost effectiveness of treatment regimen for the treatment of operable Stage IIIA-N2 NSCLC
- RecName: Full=Dynamin-1; AltName: Full=B-dynamin; AltName: Full=D100; AltName: F...RecName: Full=Dynamin-1; AltName: Full=B-dynamin; AltName: Full=D100; AltName: Full=Dynamin I; AltName: Full=Dynamin, braingi|190358918|sp|P21575.2|DYN1_RATProtein
Your browsing activity is empty.
Activity recording is turned off.
See more...