Data

The randomised trial CARDS was a trial of atorvastatin versus placebo in people with type 2 diabetes. The protocol and the characteristics of the study cohort have been described in full elsewhere.^151–153 Briefly, 132 clinical centres in the UK and Ireland recruited 2832 people with type 2 diabetes aged 40–75 years with low-density lipoprotein cholesterol ≤ 4.14 mmol/l, fasting triglycerides ≤ 6.78 mmol/l and at least one of the following conditions: hypertension, retinopathy, micro- or macroalbuminuria and current smoking status. Exclusion criteria included previous coronary heart disease or stroke, previous surgery for peripheral vascular disease, plasma creatinine ≥ 150 µmol/l, and HbA_1c ≥ 12%. Patients were recruited between 1997 and 2001. Safety parameters, including urine albumin and urine creatinine, were measured 1, 2, 3 and 6 months after randomisation, and at 6-monthly intervals thereafter. Albumin and creatinine were measured using a Hitachi 747 autoanalyser (Boehringer Mannheim Corp, Indianapolis, IN) on urine samples that were confirmed free of infection by dipstick testing. At the recommendation of the data monitoring board, the study was stopped in June 2003 following an interim analysis of the primary cardiovascular end point, which showed a highly significant (p < 0.001) benefit of atorvastatin.

Statistical analysis

As described in Chapter 3, we fitted longitudinal models for trends and variation in log-ACR. Log-ACR at diagnosis of diabetes was modelled as a patient-level, normally distributed random effect. Change over time in log-ACR was modelled as a patient-level, normally distributed random effect, correlated with actual value of ACR. Within-measurement variability in log-ACR was modelled using a t-distribution with three degrees of freedom, uncorrelated with actual level of ACR. The model parameters were estimated using WinBUGS (MRC Biostatistics Unit, Cambridge, UK).¹³⁹ We also fitted models for trends and variation in eGFR using the same methods as described above, except for the modelling of the within-measurement variability, for which we used a normal distribution. Residual plots indicated an approximate normal distribution for eGFR and, therefore, a log transformation was not required. We allowed mean eGFR and mean rate of change to vary between men and women, but held other parameters the same for men and women. Models were stratified by baseline urine albumin status. We report means and standard deviations of log- and eGFR, geometric means of ACR and the average signal-to-noise ratio as defined in Chapter 3.

Although we did not have data with which to validate individual tests for microalbuminuria in the CARDS database, the model estimates of within-person variability allowed us to estimate the proportion of positive tests that were false positive – that is, attributable to measurement variability rather than to true change in underlying renal function. With the same methodology as described in Chapter 3, we used simulation modelling to calculate the proportion of those identified with true- and false-positive tests in a population similar to that of CARDS, under the assumption of annual screening according to NICE guidelines. Our primary analysis models an annual screening programme as described above, and compares this to 2-yearly screening (biennial) and 3-yearly screening (triennial), while maintaining the NICE protocol for use of confirmatory samples when the first sample measures above threshold. In sensitivity analyses, we assess the degree of change in model parameters that would be required to reach different clinical conclusions. We also used simulation to estimate rates and accuracy of diagnoses of stage 3b kidney disease, defined by eGFR < 45 ml/minute in normoalbuminuric patients.

Albumin-to-creatinine ratio

Table 14 reports the parameters used in defining the model that estimates trends and variation in log-ACR. The mean log-ACR of 0.41 (95% CI 0.28 to 0.53) in men and 0.29 (95% CI 0.11 to 0.48) in women are equivalent to geometric mean ACR at diagnosis of diabetes of 1.51 (95% CI 1.32 to 1.70) mg/mol and 1.34 (95% CI 1.12 to 1.62) mg/mol, respectively. The average change in log-ACR per year of 0.018 corresponds to a 2% per year increase in ACR in both sexes (Figure 12). The standard deviation around this average, 0.022 on the log-ACR scale, corresponds to variation in the rate of change: the estimated 25th and 75th centiles of the annual increase in ACR are a 0.3% and 3.3% increase per year, respectively. The estimated standard deviation of within-measurement variability in log-ACR is 0.85 (95% CI 0.74 to 1.00), which corresponds to a within-measurement coefficient of variation in ACR > 100%. The average signal-to-noise ratios, defined as average change divided by within-measurement standard deviation, are therefore 0.021, 0.042 and 0.063 for annual, biennial and triennial screening, respectively.

TABLE 14

Parameter estimates (95% CIs) in a random-effects model of trend and variation in log-ACR based on the CARDS cohort

FIGURE 12

Estimated cumulative proportion of patients with microalbuminuria and macroalbuminuria drawn from a cohort based on CARDS using parameters obtained from CARDS (modelled ACR) compared with data obtained directly from the CARDS cohort. The circles and lines (more...)

Tables 15 and 16 report the estimated rates of identification of microalbuminuria modelled from these estimates. Results for men and women are shown separately (see Tables 15 and 16). The tables show the cumulative rate of positive test results, the percentage of those that are false positive and the percentage of those repeatedly testing negative that are false negative. Each of these outcomes is shown under assumptions of annual, biennial and triennial screening.

TABLE 15

Model estimates for male patients of (1) the proportions of those with type 2 diabetes diagnosed with microalbuminuria (positive tests); (2) the percentage of those diagnosed with microalbuminuria who have false-positive tests; and (3) the percentage (more...)

TABLE 16

Model estimates for female patients of (1) the proportions of those with type 2 diabetes diagnosed with microalbuminuria (positive tests); (2) the percentage of those diagnosed with microalbuminuria who have false-positive tests; and (3) the percentage (more...)

Over the first 6 years after diagnosis of diabetes, annual, biennial and triennial screening would, respectively, identify 451, 394 and 365 cases of microalbuminuria per 1000 men with type 2 diabetes. Over 18 years, annual, biennial and triennial screening would identify 582, 534 and 505 cases, respectively.

In an initial screening test, an estimated 78% of those identified with microalbuminuria would be true positive, and 22% would be false positive. By year 6, with assumptions of annual, biennial and triennial screening, respectively, 36%, 30% and 27% of diagnoses of microalbuminuria in men would be false positive, and, by year 18, 35%, 29% and 26%. By year 18, estimated false-negative rates for men were 0.1%, 0.8% and 1.7% for annual, biennial and triennial screening, respectively.

Table 16 shows the corresponding estimates for women with type 2 diabetes. Over 18 years, we estimate that annual, biennial and triennial screening, respectively, would identify 431, 382 and 354 cases of microalbuminuria per 1000 women with type 2 diabetes, 50%, 44% and 40% of which would be false positive. Of those testing negative for microalbuminuria, 0.1%, 0.3% and 0.7% would be false negative.

In summary, in men and women with type 2 diabetes, 36% (95% CI 32% to 42%) and 48% (95% CI 41% to 55%), respectively, of patients tested annually for microalbuminuria over 6 years would be inaccurately identified as having microalbuminuria. If screening intervals were extended to 3-yearly, the corresponding figures would be 27% (95% CI 23% to 31%) and 37% (95% CI 30% to 44%).

Figure 13 shows the degree to which the model reproduces the CARDS data by comparing model predictions to observed data. Figure 14 examines the extent to which the resulting model can be generalised by comparing model-predicted rates of microalbuminuria identification to observed prevalence of microalbuminuria in other cohort studies, with the limitation that different studies have used different criteria (e.g. number of confirmatory tests) for diagnosing microalbuminuria.

FIGURE 13

Estimated prevalence of normo-, micro- and macroalbuminuria, and estimated incidence of apparent regression from microalbuminuria to normoalbuminuria (dots), with 95% CIs (vertical lines), in the CARDS compared with model estimates using parameters obtained (more...)

FIGURE 14

Proportion of patients who test positive for microalbuminuria or macroalbuminuria by duration of diabetes estimated from parameters obtained from the CARDS (simulation model) compared with other cohort studies in type 2 diabetes. Bars and whiskers denote (more...)

To illustrate the sensitivity of our conclusions to the exact parameter values, Figure 15 shows how the estimated false-positive rate would vary under different assumptions about the average rate of progression of log-ACR. This illustrates the change in the number of false-positive tests when the average rate of change in ACR per year used within the model is increased above that observed in our cohort.

FIGURE 15

Sensitivity of model predictions to variation in parameter estimates. The lower line of the graph plots the percentage of positive tests that are false (numbers in the fifth column of Table 15) for males with type 2 diabetes with annual monitoring. Other (more...)

Estimated glomerular filtration rate

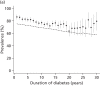
Data on 2012 CARDS participants with normoalbuminuria at baseline and 550 CARDS participants with microalbuminuria at baseline were used in obtaining model estimates. Table 17 reports the parameters used in defining the model that estimates trends and variation in eGFR in people with type 2 diabetes and normoalbuminuria. The estimated mean eGFR at 10 years since diagnosis of diabetes is 69 (95% CI 69 to 70) ml/minute in men and 62 (95% CI 61 to 64) ml/minute in women, and the between-person standard deviation is 8.7 (95% CI 8.1 to 9.3) ml/minute. The estimated average change in eGFR per year is 0.26 (95% CI 0.13 to 0.40) ml/minute in men, and 0.24 (95% CI 0.061 to 0.42) ml/minute in women. The estimated between-person standard deviation of the reduction per year is 0.50 (95% CI 0.28 to 0.69) ml/minute. The estimated standard deviation of within-measurement variation in eGFR is 4.9 (95% CI 4.8 to 5.1) ml/minute. The signal-to-noise ratio is therefore 0.053 for annual monitoring, 0.11 for biennial monitoring and 0.16 for triennial monitoring. Table 17 also shows the corresponding parameter estimates for participants with normoalbuminuria and microalbuminuria at baseline. Figure 16 illustrates the observed mean eGFR by duration of diabetes compared with the modelled estimates of progression and shows how the modelled rate of change matches the original cohort data.

TABLE 17

Parameter estimates (ml/minute) in a random effects model of trend and variation in eGFR in people with type 2 diabetes

FIGURE 16

Observed mean (dot) and 25th and 75th centiles (vertical lines) of eGFR in men (top) and women (bottom) with type 2 diabetes and normoalbuminuria, and model estimate of trends (dashed line).

Table 18 shows the modelled estimates of the proportion of normoalbuminuric men classified as having stage 3b kidney disease (eGFR < 45 ml/minute) over time for annual, biennial or triennial eGFR screening. In annual screening, for example, there would be 20 men identified with stage 3b kidney disease (95% CI 16 to 26) per 1000 after 18 years, and 67% (95% CI 53% to 83%) of these would be false positive. Similar estimates were obtained for women (data not shown).

TABLE 18

Model estimates of (1) the proportion of men with type 2 diabetes and baseline normoalbuminuria diagnosed with stage 3b kidney disease (eGFR < 45 ml/minute) (positive tests); (2) the percentage of those with positive tests who (more...)