Introduction

In Chapter 2 we discussed how to model mediational mechanisms and in Chapter 3 discussed a separate approach for analysing the effect-modifying role of post-randomisation process variables. However, in both settings we considered the situation only with a single measure of the outcome and, in general, this is unlikely to be reflective of the data available in a randomised trial. Outcome measures are usually collected at multiple time points during the follow-up period, often at the end of the treatment phase, and at least one later measurement occasion to assess longer-term effects of the intervention.

In addition, when considering mediation modelling there are often repeated measures of the putative mediator collected which could all be during the treatment phase or could extend into the follow-up phase. For example, in the MRC MIDAS trial,²¹ the putative mediator was substance misuse, and this was measured at baseline and at 6, 12, 18 and 24 months after baseline. The corresponding outcome measures of psychotic symptoms were collected at baseline and at 12 and 24 months. The mediation analysis described in Chapter 2 would consider these time points only as single measures, and does not exploit the longitudinal design of the trial or assess whether or not changes in these mediators lead to changes in the outcome.

Similarly, we can collect repeated measures of process variables, and typically these would occur during the treatment phase of the intervention. For example, in the Prevention of Relapse in Psychosis (PRP) trial,⁸¹ a measure of therapist and client empathy was completed at each session of therapy attended. Rather than picking a single session measure of empathy to consider as the post-randomisation effect modifier, using all the measures could provide additional information to more accurately model the underlying process.

This chapter will extend the methods previously described in Chapters 2 and 3 to these longitudinal data structures. We begin by considering a setting with repeated measures of a mediator and outcome, and then demonstrate how to examine mediation using growth curve models. We will redefine the B&K steps outlined in Chapter 2 for this longitudinal context. This is just one possible approach, and we describe the potential use of several other methods. Then we change focus to the analysis of process measures and first consider a single process measure (such as therapeutic alliance at a single session, as given in the SoCRATES example) with repeated measures of the outcome. Finally, we consider how to model repeated measures of the process variables (therapist empathy at each session) and consider these as post-randomisation effect modifiers of treatment effects in an extension of the principal stratification approach, which are called principal trajectories.

Extensions to repeated measures of mediators and outcomes

One of the difficulties in extending mediation analysis to longitudinal settings is that it becomes more complicated to define the question of interest, to identify which mediation parameters are of interest and to account for time-varying confounding (i.e. the confounders of the M and Y could be time-invariant or time-varying). For example, patients will enter a trial with a certain level of the mediator variable, for example substance use, which is independent of the random allocation and instead influenced by a set of other characteristics. Owing to the randomisation assumption, we assume that the mean level of substance use is the same in both arms of the trial. We hope that the intervention will lead to a greater reduction in substance use in the intervention arm than in the control arm, and that this in turn leads to a better outcome in the intervention arm. Implicitly, we are interested in the change in substance use from baseline, but at which time point? If we only have two repeated measures of the mediator, then we could continue using the methods outlined in Chapter 2 by adjusting for the baseline mediator as a potential confounder (as was illustrated in Figure 3, analogous to an analysis of covariance model). If we have several repeated measures of the mediator, we could explicitly calculate change at each of these, but this then allows for multiple mediation pathways which may complicate the interpretation of the results. Alternatively, we could consider a single change over the whole of the repeated measures using a more complicated modelling approach.

Let us consider an example with three measures of both the mediator and the outcomes and, although it is not necessary for these to be measured at the same occasion, for simplicity we denote these as occurring at the same time points. Our first step involves deciding on a suitable model for the univariate mediator measures (and likewise the univariate outcome measures), before combining these in a bivariate model with randomisation as an explanatory variable and defining the mediation pathways. MacKinnon¹⁹ (see Chapter 8) extensively discusses estimation of this three-time-point model; here we model this with a set of latent growth factors for the mediator and outcome separately, using parallel processes, and estimate the structural parameters explaining relationships between them.

For example, in Figure 4, M^t(t = 0,1,2) represents the observed mediator at time points t = 0 (baseline), t = 1 and t = 2. We are interested in modelling the relationship over time between these mediators. The univariate model is driven by the baseline levels (the random intercept, Im) and the linear change (the random slope, Sm). In Figure 4:

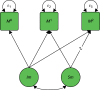
FIGURE 4

A univariate growth process for the repeated measures of the mediator M. Unlabelled paths are fixed to be equal to 1.

• The errors ε₁, ε₂ and ε₃ are independent.
• The observed scores are explained by Im and Sm.
• The means and variances of Im and Sm are freely estimated.
• The covariance between Im and Sm is freely estimated.

The next stage is to model the observed outcome in a similar way, essentially replacing M^t by Y^t in Figure 4. While it is not necessary to assume that the outcome growth process will be the same as the mediator growth process, for illustrative purposes we will make this assumption. These models are then combined in a bivariate growth model, and the treatment variable Z included as a cause of the random slope of the mediator Sm and the random slope of the outcome Sy. As Z is randomly assigned and Im represents the baseline values, we can assume that there is no covariance between Z and Im. The aim is to assess whether or not the intervention affects the growth trajectory of the mediating variable, which in turn affects the growth trajectory of the outcome variable.⁸²

This is represented in Figure 5. Here, the coefficients β₁, ψ₂ and ψ₁ refer to:

FIGURE 5

A bivariate growth process with randomised group included in the model.

• β₁, the effect of the intervention on the slope of the mediator process
• ψ₂, the effect of the mediator process slope on the slope of the outcome process
• ψ₁, the direct effect of intervention on slope of the outcome process.

Logically, these follow the same interpretation as the standard direct and indirect effects from the single-mediator/outcome approach described in Chapter 2. Since the growth factors are normally distributed latent variables, we can interpret the coefficients as being from linear models and redefine the B&K¹⁶ steps as follows:

1. Demonstrate that treatment, Z, has an effect on the slope of the outcome Sy.
2. Demonstrate that treatment, Z, has an effect on the slope of the putative mediator Sm.
3. Demonstrate that the slope of the mediator Sm has an effect on the slope of the outcome Sy after controlling for treatment Z.

As previously described, the lack of a significant total effect on the outcome in step 1 might not necessarily preclude a meaningful mediation analysis from being undertaken, if it helps to explain why a treatment was not effective. The essential criterion is step 2 because, if it cannot be shown that the treatment has influenced the putative mediator, then this cannot be on the causal pathway from treatment to outcome. As treatment is assumed to be randomised, this is an ITT analysis and so can be assessed without bias.

While this approach offers a more realistic model for the data collected in a trial and the underlying process, it suffers from the same problem as the B&K approach, namely that there could be unmeasured confounders affecting both Sm and Sy.

We demonstrated at the end of Chapter 2, in PACT, that repeated measures of the mediator can be used to avoid attenuation bias due to measurement error in a single mediator. We expect the same to apply here. The estimator of the mediation parameter ψ₂ should not be subject to attenuation bias due to measurement error in the repeated measures M^t (t = 0,1,2). Our growth model for the mediator represents a measurement model. We could make this more explicit in Figures 4 and 5 by specifying a latent true score loading onto each of these observed variables, which would be denoted as Tm⁰, Tm¹ and Tm², respectively. The growth factors would then be defined on these latent true scores. This is the focus of ongoing work and will be reported separately elsewhere.

To account for unmeasured confounding between Sm and Sy, which if present would lead to biased estimates of ψ₁ and ψ₂, one solution is, as before, allowing for correlated errors between the random slopes. This model is not identified, as we are also interested in estimating the directed arrow from Sm to Sy in order to infer mediation; however, we can take the IV approach as used previously and apply it to this model. The instruments, which could be randomisation by baseline covariate interactions as described in Chapter 2, would be assumed to influence the growth in the mediator Sm but have no direct effect on the growth in the outcome Sy. Again, this is the focus of ongoing work and will be reported separately elsewhere.

Finally, we stated that the first step in our approach to modelling repeated measures of the mediators and outcomes was identifying a suitable univariate model to describe the growth process in each of these. We demonstrated this with a linear growth curve model, but there are other possibilities too. These include piecewise growth models, change score models and autoregressive models. Many of these are discussed in MacKinnon,¹⁹ Muthén and Khoo,⁸³ and McArdle.⁸⁴ They follow the same procedure as described with the growth curve model but produce different measures of ‘change’, and so they lead to different driving variables and different interpretations of which aspect of the mediator is changing which aspect of the outcome. We will not explore these models in more detail here, but instead now consider alternative longitudinal extensions.

Extensions to repeated measures of outcomes with a single-process measure

In Chapter 3, we introduced principal stratification for assessing how treatment effects vary depending on the latent principal stratum. This treated the process measure, such as therapeutic alliance, as a post-randomisation effect modifier. Recall that the strata are partially observed, remaining hidden in the control group but identifiable in the treatment group where the process measure is observed; our approach relies on having good predictors X of the strata membership. In our previous SoCRATES example, we considered only a single outcome measure, the PANSS score at 18 months; now we consider the situation where we have repeated outcome measures.

In the previous section we introduced the latent growth curve model (see Figure 4). Here, we demonstrate how GMMs can be applied to account for repeated measures of the outcome. We will use a finite mixture model approach to estimate the proportion of patients in the latent classes (principal stratum). Then we fit separate random coefficient models to the outcome data within each principal stratum using maximum likelihood estimation, to assess if the effect of random allocation on the slope of the outcome varies by latent class. The question of interest within these models is ‘how is the effect of treatment on the growth parameters influenced by the different latent classes or principal strata?’.

We simultaneously fit the following models using maximum likelihood with the EM algorithm:

1. Fit a latent class model (the latent classes being the principal stratum) using the single measure of the process variable and baseline covariates to predict class membership.
2. Within each of the above latent classes (principal strata), fit a growth curve for the repeated measures of the outcome.
3. Evaluate the effects of the intervention on the growth parameter (slope) within each class.

We can test whether or not the effects of the intervention on the slope parameters are the same within each stratum by introducing and evaluating the introduction of between-stratum using constraints. The combined model is an example of a GMM.

The model is shown in Figure 6. Here, since A is a categorical latent variable, the interpretation of this GMM is not the same as for a continuous latent variable. The arrows from A to the growth factors indicate that both the intercepts and slopes vary with A (i.e. A has a prognostic effect on outcome), as well as being influenced by the baseline covariates X. In addition, the arrow from A to that of the effect of randomisation (Z) on the slope factor indicates that A is a treatment effect modifier.

FIGURE 6

Growth mixture model for repeated outcomes within principal strata.

In the context of CACE estimation (as described in Chapter 1), Muthén and Brown⁸⁵ have investigated the use of latent growth curve or trajectory models for repeated measures of outcomes with a single measure of compliance; it is this approach we extend using alternative process measures rather than compliance.

Recently it has been pointed out that such a one-step approach ‘can be flawed because the secondary model for the outcome may affect the latent class formation and the latent class variable may lose its meaning as the latent variable measured by the indicator variables’.⁸⁶ The authors describe an alternative three-step approach, in which the latent class model is estimated in the first step based on the latent class indicator variables only, independently of the outcome variables and its model. This has some appeal in our current context, as we would want to form latent classes based on the process variables which do not change with the outcome being analysed; however, this three-step approach has only recently been incorporated into Mplus, and further work is needed to compare with the one-step approach in our work.

SoCRATES example

Following the analysis of the SoCRATES trial presented in Chapter 3, in which we considered the therapeutic alliance at the fourth session of therapy as our process variable, we can postulate the existence of two principal strata:

• High-alliance participants: those observed to have a high alliance in the therapy group together with those in the control group who would have had a high alliance had they been allocated to receive therapy.
• Low-alliance participants: those observed to have a low alliance in the therapy group together with those in the control group who would have had a low alliance had they been allocated to receive therapy.

Rather than estimate the treatment effect on the outcome measured only at 18 months, we acknowledge that we have five repeated measures of PANSS outcomes in SoCRATES. These were measured at baseline (time score 0), 6 weeks (time score 1.94591), 3 months (time score 2.5649493), 9 months (time score 3.6109178) and 18 months (time score 4.3694477). In the analyses we log transformed the time scale as measured in weeks, which is shown in parenthesis above.

We simultaneously fit the following models using maximum likelihood with the EM algorithm:

1. principal stratum membership on the baseline covariates: logDUP, centre, years of education
2. linear growth model within each class, allowing all the random-effect means and variances to vary between high- and low-alliance classes
3. effect of randomisation on the slope within each class.

The procedure was bootstrapped to obtain valid SE estimates, and the method allows for missing data under a MAR assumption. Figure 7 shows the observed trajectories and the estimated mean PANSS score at each time point for the 63 subjects assigned low-alliance class. Figure 8 shows the observed trajectories and estimated mean PANSS score for the 138 subjects in the high-alliance class.

FIGURE 7

SoCRATES: estimated mean and the observed trajectories for low-alliance class (n = 63).

FIGURE 8

SoCRATES: estimated means and observed trajectories for high-alliance class (n = 138).

The results for the effect of randomisation on slope by principal stratum are as in Table 6.

TABLE 6

SoCRATES: estimates of the effect of randomisation on slope by principal stratum

We reach similar conclusions to those found in the analysis in Chapter 3: in the high-alliance class there appears to be a beneficial effect of the treatment but in the low-alliance class there is a non-significant but detrimental effect of treatment compared with control.

Extensions to repeated measures of process measure: principal trajectories

In Chapter 3, we demonstrated how the principal stratification approach can be used to analyse process measures with a single time point. However, in many of our randomised trials, we collect the process measures at each session of treatment. For example, in the PRP trial of CBT, the patients rated their empathy with the therapist at each session of CBT they attended. The control group received TAU so there was no corresponding measure of empathy that could be observed in the control group. To use the principal stratification approach, we would have to select a session of therapy and use the empathy value from the treatment group at that session; this is clearly not making the most efficient use of all the available data.

Here we propose a new extension to principal stratification, termed principal trajectories, that makes efficient use of the repeated measures of process variables and can also allow for participants with missing data or who drop out of the intervention. In summary, we estimate general GMMs on the repeated measures of the process variables in the intervention group using maximum likelihood, assigning participants to hypothesised latent trajectory classes by estimated posterior probabilities. Using baseline covariates which predict class membership, we assign which class the control group participants would have been in, had they been randomised to intervention. We then examine the effect of random allocation on outcome within each class. If required, an exclusion restriction of no treatment effect within one of the latent classes can be imposed to aid identification.

To illustrate this approach, first we consider the simpler scenario of repeated measures of only one variable, for example the mediator or outcome, and reintroduce the idea of the latent trajectory model. In this form, the random part of the model is represented by discrete trajectory classes A_c with probability of class membership π_A and by a separate intercept and slope estimated in each class. This scenario is shown hypothetically in Figure 9; the left-hand panel shows individual trajectories of empathy over therapy sessions and the right-hand panel shows these trajectories have been grouped into distinct latent classes (in this case, two classes).

FIGURE 9

Individual trajectories grouped into latent classes (principal trajectories).

However, these trajectories and classes can be produced only for the treatment group, as there is no measure of empathy in the control group. We need to make an inference about the empathy trajectory of members of the control group had they been randomised to the treatment group. We could either infer the trajectories themselves or assign an empathy class membership to the patients in the control group, based on the observed trajectory classes from the treatment group. This latter approach relies on there being good baseline predictors of class membership, as with the principal stratification approach.

There are two options for proceeding when we have calculated the potential trajectories for each subject:

1. Within classes, separate models can be fit investigating the relationship between randomisation and outcome. This can be either a straightforward ITT effect based on a regression model or more complicated models allowing for repeated measures in the outcome variables as well. The differences in the coefficients for randomisation between the classes can be interpreted as providing evidence for different between class treatment effects.
2. Rather than forming the latent classes on just the mediator trajectories, we could combine these with outcome trajectories, and form latent classes based on both the mediator and outcome trajectory patterns (involving estimating shared growth parameters).

Figure 10 shows a latent variable model illustrating the first of these scenarios: Ac represents a categorical latent variable which determines the growth terms Iy and Sy; Ac is predicted by baseline covariates X, and the effect of randomisation Z on Y is modified by Ac.

FIGURE 10

A latent variable model illustrating the principal trajectories approach. A latent variable model illustrating the principal trajectories approach.

The full principal trajectories estimating procedure is outlined as follows:

1. For the repeated process measures in the treatment group, examine the pattern of the observed trajectories and assess variation between participants.
2. Fit GMMs using maximum likelihood to find principal stratum (latent trajectory classes).
3. Assign participants in the intervention group to the most likely principal stratum (latent class) using estimated posterior probabilities.
4. Use an appropriate regression model to examine baseline predictors of stratum/class membership.
5. Use the estimated parameters from this regression model to assign the control group participants to the stratum (latent class) they would have been in, had they been randomised to the treatment group.
6. Examine the effect of treatment (i.e. randomisation) on outcome within each stratum/class separately. An exclusion restriction can be imposed here in order to aid identification.

Example: the Prevention of Relapse in Psychosis trial

The primary analysis of the PRP trial showed that neither the CBT nor the Family Intervention groups had an effect on remission, relapse or days in hospital compared with TAU but that CBT had a beneficial effect on depression scores (BDI) at 24 months compared with TAU alone.⁸¹ The CBT intervention and family intervention for psychosis focused on relapse prevention for 20 sessions of therapy over 9 months, with the therapist–client empathy measured by the client at each session (where a high score is better). For this analysis, we compare the CBT + TAU group with the TAU alone group. We applied the principal trajectories steps outlined above using Mplus version 7.11, with the one-step maximum likelihood estimation procedure. This led to the following results:

1. a linear mixed model (random slope and intercept) fits the observed shape of trajectories in the CBT group
2. two distinct latent classes found (class 1, always high empathy; and class 2, improving empathy)
3. 76 CBT clients were assigned to class 1 and 16 were assigned to class 2
4. baseline predictors were carer involved in treatment (yes/no), centre, depression outcome (BDI), gender, outpatient status (yes/no)
5. total of 176 clients assigned to class 1, 46 assigned to class 2 (entropy = 0.71)
6. compare BDI scores at 12 and 24 months between CBT versus TAU.

Our model found two classes, which subjectively we call an ‘always high’ class, and an ‘improving’ class. Figure 11 shows the observed mean scores and the model predicted mean scores for the empathy measure at each session, by latent class. The estimated ITT effects within classes for CBT compared with TAU on BDI scores common at 12 and 24 months are shown in Table 7, where a negative effect indicates CBT improves BDI.

FIGURE 11

Example of principal trajectories in the PRP trial, with two latent classes.

TABLE 7

Estimated ITT effects for CBT compared with TAU on BDI scores common at 12 and 14 months

Although the results are not conclusive and do not achieve statistical significance, it suggests that in the ‘improving’ class the treatment effect is larger and in the expected direction of CBT being superior, whereas in the ‘always high’ class the CBT does not appear to be superior to TAU. One could construct a post-hoc justification for this; that those clients in the always-high group might have characteristics that suggests their outcome will be good regardless of their treatment allocation, and so the CBT does not have an effect. This suggests that empathy may have a causal role in explaining treatment effect heterogeneity; however, further, ongoing work is needed to verify these findings and so these should be interpreted with caution. At present, they serve as a real illustration of our proposed new method.