Included under terms of UK Non-commercial Government License.
NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.
Hind D, Parkin J, Whitworth V, et al. Aquatic therapy for children with Duchenne muscular dystrophy: a pilot feasibility randomised controlled trial and mixed-methods process evaluation. Southampton (UK): NIHR Journals Library; 2017 May. (Health Technology Assessment, No. 21.27.)

Aquatic therapy for children with Duchenne muscular dystrophy: a pilot feasibility randomised controlled trial and mixed-methods process evaluation.
Show detailsImplementation of the intervention and trial
Implementation summary
Overall, 17 sites were approached to participate in the study: six sites opened and 11 were unable to do so. Of the six sites involved in the grant application, four opened between October 2014 and December 2014, one was unable to proceed because of difficulties securing treatment costs and another because of pool access. Ten sites approached between December 2014 and May 2015 either declined or were unable to gain the relevant approvals in time. Reasons for non-involvement included treatment costs, a lack of eligible participants within travelling range, lack of AT pool availability, organisational change (e.g. moving premises) and therapists being on maternity leave. In April 2015, two additional sites were initiated. The duration between site initiation and the first participant consent was 30–40 days for two sites, 50–60 days for another two sites, 90 days for one site and 169 days for another site.
NHS treatment costs as a cause of centre attrition
Considerable problems were encountered in accessing treatment costs for the research. Where the cost of an experimental treatment is greater than the cost of usual care, in the UK this cost falls on health-care commissioners rather than grant-awarding bodies.185 Although at the time at which the trial was run most NHS commissioning was devolved, local commissioners recognised that the commissioning of services for rare disease groups was the responsibility of NHS England, an executive non-departmental public body of the Department of Health, established in 2013. However, NHS England responded that they did not have a process in place to support the alignment of commissioning priorities and research needs and refused to meet the treatment costs. After negotiating for several months with local commissioners, one of the original sites withdrew from participation in the study because they could not meet the treatment costs for the trial locally [minutes, Trial Management Group (TMG), 19 January 2015]. Neither local commissioners nor the participating trusts effectively met the treatment costs at other trusts, with physiotherapy teams absorbing the costs within their units or, more usually, participating physiotherapists delivering the intervention and trial procedures in their own time (see Chapter 5, Therapist views of the service, Operational work and Chapter 5, Comments on the trial procedures, Operational work). This was possible only because of the low levels of recruitment and the goodwill of research enthusiasts in research-active trusts.
Specialist centres and distance from the target population
The use of highly specialist physiotherapists from tertiary centres to deliver the AT intervention proved problematic. The eligible patients who were approached for participation in a RCT, which could see them come into the centre twice per week, would have to travel for long distances. Eligible participants at Leeds lived as far afield as Hull and York; Great Ormond Street Hospital, London, drew its patients from as far as Watford and Guildford. At other centres, the majority of study candidates lived > 20 miles away. Unlike in a previous paediatric AT trial, in which usual care involved a 2-week inpatient stay in a specialist centre, at the beginning of which children could be randomised, the contemporary DMD treatment pathway was wholly based on outpatient visits. The team at Great Ormond Street Hospital planned to deliver the intervention not on their own premises, but at AT suites in east and north-west London, which were closer to, and more accessible for, the target population (minutes, TMG, 7 July 2014). However, on investigation, the costs proved prohibitive (minutes, TMG, 3 November 2014). The inability to reimburse travels costs for travel to intervention sessions caused some consternation (minutes, TMG, 7 July 2014).
The idea of subcontracting delivery of AT to therapists at satellite centres, nearer to participants’ homes was discussed (minutes, TMG, 7 July 2014, 19 January 2015). However, given that the population is small and geographically dispersed, we have had to contract with almost as many community trusts as participants would, not to mention agree treatment costs (see previous paragraph) for interventionist training and the delivery of the intervention. The team’s perception was that less research-active community trusts were less likely to tolerate implementation of the study and intervention without access to treatment costs. All trusts had intended to run AT as a group intervention with two or more children in the pool, something that was prevented by under-recruitment. All the trusts were limited to providing AT sessions in office hours because of staffing requirements for safety and evacuation procedures and lone-working policies (minutes, TMG, 3 November 2014).
Participant recruitment and the prohibition on co-enrolment
The general prohibition on co-enrolment of patients,186 especially those deemed to be vulnerable, considerably reduced the pool of candidates available to the study. For instance, at Great Ormond Street Hospital, the children with the best cardiac function tended to be already enrolled in the DMD Heart Protection Study (ISRCTN50395346), meaning that the potential sample could have poor external validity. In addition, there were concerns that many parents were anticipating the opening of well-advertised drug studies (NCT02383511, NCT02369731, NCT01957059, NCT01826474) and would withhold their children from the AT trial, or enrol and then drop out, in the hope of access to a disease-modifying drug therapy (minutes, TMG, 7 July 2014). Although the NIHR urged us to co-enrol patients who had already consented to drug trials (Emma Catlin, NIHR, 2013, personal communication), the research ethics committee refused our request to do so (Leslie Gelling, NRES Committee East of England-Cambridge South 2014, personal communication).
Problems with the delivery of land-based therapy
The commissioning brief required that LBT be ‘optimised’. Normally, community physiotherapists see families between once every 6 weeks and once every 6 months to give an exercise prescription (the minority of patients that are at special schools have therapists who come into school to deliver exercises two or three times per week). Specialist physiotherapists on the team felt that the delivery of LBT would be variable between participants in between seeing community physiotherapists. In routine practice, specialist physiotherapists can recommend problems to work on and specific techniques to community physiotherapists, but varying degrees of co-operation between specialist and community physiotherapists were reported. The reorganisation of services in 2013, when this research was commissioned, following the Health and Social Care Act 2012,187 resulted in complexity and a lack of uniformity of services previously hosted by primary care trusts, including community physiotherapy.188 As we anticipated difficulties finding out with whom to engage and approach, in order to gain the appropriate NHS Research and Development permissions to implement the study, we asked physiotherapists at participating specialist centres to prescribe LBT for the duration of the trial (minutes, TMG, 15 September 2015). We then relied on parents to capture the weekly delivery of LBT on a log.
Problems with data collection
The ability to deliver the 6MWD, which requires a 30-m corridor,189 was a source of great anxiety in the set-up period. Some hospital sites, where the NSAA would normally have been conducted, did not have passageways of this length (minutes, TMG, 7 July 2014, 15 September 2014, 3 November 2014). It was also posited that, in trusts that were not research active, training would have to be given regarding the administration of the 6MWD (minutes, TMG, 15 September 2014). Although the costs of data capture and entry were adequately funded, this money did not translate into extra resource for the units in terms of a data entry clerk at any of the sites. Instead, relatively expensive physiotherapists ended up entering data, with the CTRU personnel team making on-site visits to help out as the trial advanced (minutes, TMG, 3 November 2014).
Recruitment and participant flow
The first site was initiated on 24 October 2014 (Figure 9). All sites were instructed to cease consenting new patients when recruitment closed on 30 June 2015, so that those consenting could be randomised by 31 July 2015 because of the need to take two NSAA scores 1 month apart (see Chapter 2, Participants). The first patient was consented on 23 December 2014 and randomised on 10 February 2015. The last patient was consented on 24 June 2015 and randomised on 17 July 2015. The trial ended as planned when the window for 6-month follow-up closed on 28 January 2016. In 40 centre-months we consented and randomised 12 participants (0.3 per centre-month), of whom 10 have 6-month follow-up data for the NSAA and between five and nine have 6-month follow-up data for other outcomes. The six sites screened 348 boys for eligibility, of whom only 17 were interested and eligible (Figure 10). Thirteen were formally screened and consented (32.5% of the recruitment target, n = 40), and 12 were randomised (30% of the recruitment target, n = 40). Eight participants were randomised to AT plus LBT and four to LBT alone.

FIGURE 9
Number of participants randomised by month.
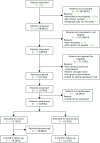
FIGURE 10
Participant flow diagram.
Protocol non-compliances
Table 6 shows protocol non-compliances. In general, these were to do with the timing of assessments not being within acceptable ‘windows’. Issues with consent included getting verbal but not written assent at the same time as consent and using superseded versions of consent/assent forms.
TABLE 6
Protocol non-compliances summary
Losses and exclusions after randomisation
Table 7 shows the pilot trial completion rate by site. One of the 13 boys for whom the study team received parental consent withdrew from the study before randomisation; his family could not be contacted to confirm the reason, which was, according to a physiotherapist, to enter a drug industry trial. Two participants formally withdrew from the study before completing, both from the control arm: one gave the reason as ‘burden of attending the trial procedure for child’ (R06/001), the other was ‘accepted onto another trial’ (R01/001). One participant was lost to follow-up in the control arm (R07/002). No patients were excluded by the study team.
TABLE 7
External pilot trial completion summary
Baseline data
Demographic and social and schooling information for randomised participants is displayed in Tables 8 and 9, respectively.
TABLE 8
Demographics
TABLE 9
Social and schooling information
Feasibility outcomes
Owing to reporting guidelines, several protocol-specified feasibility outcomes sit more comfortably elsewhere in the report. For information on eligible patients approached for the study, see Recruitment and participant flow. For reasons for refused consent and participant attrition rate, see Losses and exclusions after randomisation. Reasons for attrition from the research protocol are detailed in Losses and exclusions after randomisation. Participant and parent views on the feasibility and acceptability of the intervention can be found in Chapter 5, Context understood through the International Classification of Functioning, Disability and Health – Child and Youth version and burden of treatment theory and Patient and parent views of the aquatic therapy intervention; those of the therapists can be found in Chapter 5, Therapist views of the service analysed within normalisation process theory. Participant, parent and therapist views on the acceptability and feasibility of the research protocol can be found in Chapter 5, Comments on the trial procedures. We did not consult, as originally stated in the protocol, therapists on the risk of control arm contamination after understanding how technical, and therefore impossible to replicate without training, the intervention was. The feasibility of recruiting participating centres is addressed in Implementation of the intervention and trial and the estimation of costs is addressed in Chapter 6. Finally, intervention optimisation (in place of intervention fidelity) is addressed in Chapter 4.
Decision on the primary end point and sample size for a full-scale trial
Although the 6MWD is the most popular primary outcome in drug trials for ambulant children with DMD, the study raised concerns about its feasibility (see Problems with data collection). Such concerns would be magnified if, as seems likely, any future study involved community trusts, which are more likely to lack the necessary 30-m corridors for the shuttle walk or staff already trained in assessment. For this reason, the NSAA, which is routinely collected for all boys with DMD in the UK, seems like the most feasible outcome for any future full-scale trial. Not only could data collection costs be minimised through its use, but, given the small number of DMD patients available, it is essential that we minimise any loss of information – especially in the control arm – as a result of patient attrition.
Table 10 lists the maximum sample sizes and expected sample sizes on termination required by three-stage ρ-family error spending tests of H0. We fix the power to detect a minimum important difference of 9 points at 0.8, and take the response SD to be 15 points, which looks sensible given the results of Mayhew et al.190 We consider designs for a range of values for the type I error rate; given the small sample sizes available, we may be willing to conduct a trial at higher than conventional significance levels, acknowledging the increased risk of a false-positive conclusion when interpreting the trial results.
TABLE 10
Frequentist sample size calculation
To interpret the numbers listed in Table 10, please note that once a patient enters the trial, there will be a 6-month delay before their primary response to treatment can be measured. As a result of this delay, when the trial is conducted, at each interim analysis there will be patients in the pipeline who have not yet been followed up for their 6-month response. Conservatively, this external pilot indicates that a future trial might recruit up to 16 boys per year, which implies that approximately eight boys would be in the pipeline at an interim analysis. The standard group sequential designs summarised in Table 10 make stopping decisions using only those data available at an interim analysis. However, the expected sample sizes listed are the expected numbers of patients recruited on termination, incorporating those who are in the pipeline when a stopping decision is made.
From Table 10 we see that the maximum sample sizes needed to conduct a definitive trial with a conventional type I error rate of α = 0.025 are likely to be prohibitive in the context of a national UK trial, which could recruit up to 16 boys with DMD per year. At this rate of recruitment, it would take > 6 years to reach the maximum sample size in the absence of early stopping. If we relax the type I error constraint to test at the 10% significance level, we would expect to take around 2.5 years to come to a conclusion and, in the absence of early stopping, just under 4 years to recruit the maximum sample size.
Table 11 summarises the findings of a simulation study, listing the percentage of trials satisfying the proposed success criterion for various sample sizes when prior distributions are as previously defined. The frequentist type I error rate at θ = 0 is approximately 10%, which is much higher than the conventional 2.5% significance level permitted for one-sided tests of superiority. Under the assumptions of the simulation study, we estimate that a future Bayesian trial would have frequentist power of ≥ 0.7 to detect a clinically relevant treatment effect if ≥ 40 patients could be recruited and followed up for their primary response at 6 months.
TABLE 11
Sample size calculation for Bayesian design
Results are based on 10,000 simulations. N is the total sample size divided equally between interventions. Data are simulated according to the model ∼ N(θ, 4σ2/N) and s2 ∼ (σ2/N) χN − 22 setting σ = 15 and δ = 9.
Delivery and receipt of the aquatic therapy and land-based therapy interventions
If eight participants allocated to AT attended all 52 AT sessions, there would be 416 session reports. In fact, several participants did not have their first AT session until some time after randomisation (Table 12). The median time between randomisation and commencement of AT was 47 days (range 7–211 days); the mean was 63 days. As a result, not all 416 sessions were possible, especially for those randomised late in the project because the 6-month assessment is anchored to the randomisation date. Of the 349 scheduled sessions for which we have data, 203 (58.2%) expected sessions took place and 146 (41.8%) did not. Reasons for aggregate non-attendance are reported in Table 13 (for individual non-attendance, see Chapter 4, Attendance). Where reasons for session cancellation were discernible (10% of sessions were unaccounted for), there was an even split between participant/family factors (43%) and health-care provider factors (47%).
TABLE 12
Time to first AT session and number of sessions by participant
TABLE 13
Aquatic therapy session attendance by centre
Of the 12 participants who were randomised, only five returned any LBT data, and for one of those there was only 1 week’s worth of data (Table 14). The other four participants returned more or less full sets of data. The median duration between randomisation and the first date on a LBT parent-completed data collection form was 25 days (range 11–52 days); the mean was 28 days. The LBT adherence data completion summary is shown in Table 15.
TABLE 14
Time to first recorded LBT session and number of sessions by participant
TABLE 15
Land-based therapy adherence data completion summary
Clinical outcomes and estimation
In the statistics that follow, a difference in means starting with a zero reflects a direction of effect that would favour AT, were the trial adequately powered; those starting with a ‘1’ would favour the control arm. Owing to control arm attrition, comparative statistics are presented for the NSAA only. NSAA measures of functional exercise capacity are shown in Figure 11, in which we include the observed average annual decline in function on the NSAA scale for UK boys diagnosed with DMD aged > 7 years, calculated as 3.7 units per year.72 Therefore, over the study period of 6 months, the expected decline for the boys in our sample is estimated to be 1.85 units. On average, the 12 study participants who were randomised had a NSAA value of 24.75 and would be expected to have an estimated value at 6 months of 22.9 units. The mean score at 6 months was 21.0 (SD 15.6) in the control arm (n = 2) and 21.4 (SD 8.5) in the AT arm (n = 8), a difference of –0.38 (95% CI –17.95 to 17.2). The mean change score was –5.5 (SD 7.8) in the control arm and –2.8 (SD 4.1) in the AT arm, a difference of –2.8 (95% CI –11.3 to 5.8). The clinical outcomes are displayed in Table 18 and the change in 6MWD over 6 months is shown in Figure 12.
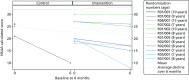
FIGURE 11
North Star Ambulatory Assessment scores.
TABLE 18
Clinical outcomes

FIGURE 12
Change in 6MWD over 6 months.
Figures 13 and 14 show the FVC absolute and FVC percentage predicted for height, respectively.

FIGURE 13
Forced vital capacity absolute.

FIGURE 14
Forced vital capacity percentage predicted for height.
Figures 15 and 16 display the CHU-9D and CarerQol scores over 6 months, respectively.
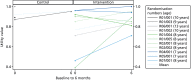
FIGURE 15
Child Health Utility 9D Index.

FIGURE 16
Care-related quality of life.
Adverse events
A total of 15 adverse events were reported to the trial team (Table 19). The only event related to the intervention was delayed muscle soreness, which was expected. Of the rest, 10 were falls related, two were related to influenza immunisation and the remainder were related to chest infection and sleep hypoventilation. There were no serious adverse events. In addition, two parents reported back pain, which they attributed to home delivery of LBT exercise (see Chapter 5, Fatigue and pain). Post-AT pain, as measured on the Wong–Baker pain inventory, and fatigue, as measured on the Children’s OMNI Scale of perceived exertion, are addressed in Table 20.
TABLE 19
Adverse events experienced by children in the trial
TABLE 20
Wong–Baker Pain and OMNI fatigue scores after AT
Sample size calculations for candidate future trials
We calculated a sample size calculation for a full-scale trial comparing optimised LBT versus LBT plus AT for boys with DMD. Based on feasibility data, we assumed that the primary end point would be the NSAA score at 6 months from randomisation (see Problems with data collection and Decision on the primary end point and sample size for a full-scale trial). The linearised version of this score was used with transformed scores lying between 0 and 100.190 This is preferred to ensure that a unit change in score implies the same change in function across the breadth of the scale. We restricted our attention to frequentist and Bayesian designs for randomised designs. It may be difficult to learn about the effectiveness of AT from observational studies, as patients will receive varying background therapies of glucocorticoid steroids, which may influence disease progression. The designs were proposed under the simplifying assumption that linearised NSAA scores are approximately normally distributed. When performing sample size calculations, we take a minimum important treatment effect to be a 9-point change on the transformed NSAA scale.
Frequentist group sequential trial
In the following, we refer to optimised LBT and LBT plus AT as interventions C and E, respectively. We assume that transformed NSAA scores at 6 months would be analysed by fitting a general linear model adjusting for baseline NSAA score and other relevant baseline covariates. Therefore, the 6-month response of the ith patient would be modelled as:
where XEi is an indicator variable that takes the value 1 if patient i is randomised to the intervention, and 0 otherwise; XBi is the NSAA score at baseline; and εi is an independent random-error term with εi ∼ N(0, σ2). We interpret θ as the adjusted difference between expected transformed NSAA scores at 6 months on E versus C; positive values indicate that E is superior to C.
Our first proposal is to conduct a future trial according to a group sequential test of H0: θ ≤ 0 against H1: θ > 0 with type I error rate α at θ = 0 and type II error rate β at θ = δ. We take δ = 9 as the minimum important difference we wish to detect. We shall consider group sequential designs, which permit early stopping either for futility (i.e. to abandon a lost cause) or for success (i.e. to declare E superior to C). By testing the H0 group sequentially, we reduce the expected number of patients needed to conduct the trial, which is particularly desirable in this context when sample sizes are small. We consider one-sided, rather than two-sided, tests of null hypotheses as AT would be adopted in practice only if it can be shown to be superior to standard care.
We propose group sequential tests of H0 following error spending designs, so called because stopping rules are derived such that certain probabilities of making a type I or type II error are ‘spent’ at each interim analysis. The advantage of this type of design is that it can accommodate unpredictable group sizes, which are likely to occur if recruitment rates are unpredictable and Data Monitoring and Ethics Committee meetings are scheduled at fixed calendar times. We consider designs spending error probabilities according to the ρ-family of functions:
where t, 0 ≤ t ≤ 1, represents the fraction of the test’s maximum information level that has been accrued. Here, f and g stipulate the cumulative type I and type II error probabilities to be spent by the time information fraction t has been accrued. The error-spending parameter, ρ, governs how rapidly error probabilities are spent as a function of the statistical information available for θ: smaller values of ρ imply more aggressive stopping rules with greater opportunity for very early stopping.
Bayesian design
We could shift the aim of a future trial from reaching definitive conclusions on the relative merits of interventions E and C to increasing our understanding of these merits. A future trial would then proceed by recruiting as many patients as possible over a reasonable time frame; based on the HydroDMD pilot study, we believe that 32 patients could be recruited over 2 years. The accumulated data would then be analysed using Bayesian methods to quantify our current thinking about treatment benefits.
Before the future trial begins, the Bayesian approach would start with a thorough evaluation of what is already known about probable patient responses on interventions E and C. For simplicity, we shall take µE and µC to represent the average change from baseline to 6 months in the linearised NSAA score on interventions E and C, respectively. Furthermore, let σ2 denote the common variance of the change from baseline scores. We propose that our prior understanding of the relative merits of interventions E and C could be summarised by placing the following independent prior distributions on θ = µE – µC and σ:
The prior for θ summarises the findings of the HydroDMD pilot study: the mean is equal to the observed sample mean difference while we set the prior SD equal to twice the estimated standard error of the sample mean. This inflation is made in order to downweight the contribution of the pilot information to a future efficacy trial and reflects our uncertainty about the estimated standard error. An independent and vague prior is used for σ to reflect our uncertainty about the response variance. We could seek to incorporate into the stated prior distributions data from other relevant historical controlled trials; however, the natural history of DMD is known to have changed markedly in recent years with the introduction of glucocorticoid therapy and the standardisation of usual care (Ricotti et al.72). Therefore, it is unlikely that the average responses seen in historical trials would be commensurate with those seen in contemporary studies.
The next step would be to conduct the Bayesian trial, recruiting as many patients as possible across a network of UK centres. Patients would be randomised in a 1 : 1 ratio between interventions E and C. On termination of the trial, once all recruited patients have been followed up for their 6-month outcome, the new trial data would be summarised by the pair of sufficient statistics for θ and σ, that is, the maximum likelihood estimate of θ and the sample variance. A Bayesian analysis would then be performed, using Bayes’ theorem to update the priors to derive posterior distributions incorporating the trial data. A provisional decision to introduce intervention E would be made if the posterior probability that θ > 0 exceeds 0.9.
Figures 17 and 18 show the OMNI after the session and change for each intervention participant, respectively.
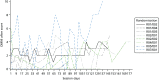
FIGURE 17
OMNI score after the session.

FIGURE 18
OMNI score change.
Figures 19 and 20 show the Wong–Baker visual analogue scale after the session and change for each intervention participant, respectively.

FIGURE 19
Wong–Baker visual analogue scale after the session.

FIGURE 20
Wong–Baker change.
- Results of the pilot trial - Aquatic therapy for children with Duchenne muscular...Results of the pilot trial - Aquatic therapy for children with Duchenne muscular dystrophy: a pilot feasibility randomised controlled trial and mixed-methods process evaluation
- Results - The effectiveness, acceptability and cost-effectiveness of psychosocia...Results - The effectiveness, acceptability and cost-effectiveness of psychosocial interventions for maltreated children and adolescents: an evidence synthesis
- Cost analysis - Aquatic therapy for children with Duchenne muscular dystrophy: a...Cost analysis - Aquatic therapy for children with Duchenne muscular dystrophy: a pilot feasibility randomised controlled trial and mixed-methods process evaluation
- Summary of findings and assessment of feasibility - An intervention to improve t...Summary of findings and assessment of feasibility - An intervention to improve the quality of life in children of parents with serious mental illness: the Young SMILES feasibility RCT
- Results - A high-dose preparation of lactobacilli and bifidobacteria in the prev...Results - A high-dose preparation of lactobacilli and bifidobacteria in the prevention of antibiotic-associated and Clostridium difficile diarrhoea in older people admitted to hospital: a multicentre, randomised, double-blind, placebo-controlled, parallel arm trial (PLACIDE)
Your browsing activity is empty.
Activity recording is turned off.
See more...