Condition-specific and generic instruments

Cost-effectiveness analysis is a comparative assessment of both costs and benefits linked to health-care interventions. Evidence of the benefits is often synthesised from clinical trials and may be captured as HRQoL using either ‘condition-specific’ or ‘generic’ survey instruments. Condition-specific instruments focus on health dimensions relevant to a particular disease, whereas generic instruments assess core dimensions of health that are relevant to all conditions.⁴⁹ Clinical trials often use condition-specific instruments as an outcome measure because these instruments are focused on the specific domains of QoL that are affected by a condition and are, therefore, sensitive to treatment effect in these domains. On the other hand, generic instruments measure a broader HRQoL construct;⁵⁰ therefore, they allow comparisons of treatment benefit across a wide range of interventions across multiple conditions. Furthermore, generic instruments can be classed as either ‘preference-based’ or ‘non-preference-based’.

Preference-based versus non-preference-based instruments

Preference-based generic instruments attach weights to the domains of health to reflect a stronger preference for one domain of HRQoL over another, in order to generate a single weighted score, also known as a utility score.⁵¹ In contrast, non-preference-based instruments simply sum the scores from all the health domains and, thus, assume an equal weighting. For cost–utility analysis, preference-based generic instruments are required to measure QoL, from which utility can be derived. The majority of generic instruments used in clinical trials are non-preference based,⁵² and are consequently of limited use for estimating the cost-effectiveness of diverse interventions on a common scale.

Validity of Child Health Utility 9D and Pediatric Quality of Life Inventory questionnaires across paediatric age groups

To capture both length and QoL associated with treatment, economists use QALYs,^53,54 whereby cost-effectiveness of the treatment is expressed as cost per additional QALY gained. Within paediatric medicine, however, most HRQoL instruments developed for children and adolescents are non-preference based⁵⁵ and, therefore, cannot be used for economic evaluation⁵⁶ when QALYs are the desired outcome. However, a prediction algorithm/mapping function can be used to predict utility scores from responses to a non-preference-based instrument. This algorithm reflects the relationship between the preference and the non-preference-based instrument, using responses from a prior population.

Rationale for mapping within the PREDNOS study

Participants recruited into the study were aged between 2 and 15 years at baseline, with the oldest participant being 18 years old at the last follow-up. Therefore, in order to generate utility values for the2- to 18-year-olds within the trial, HRQoL information was collected either from both the PedsQL and the CHU-9D questionnaires for participants aged ≥ 5 years or from just the PedsQL instrument for participants aged 2–4 years. Therefore, utility values were directly elicited for all participants aged ≥ 5 years; for participants aged 2 to 4 years, the mapping algorithm was applied to predict the CHU-9D utility score based on the responses to the PedsQL instrument.

Outcome measures

The CHU-9D questionnaire was initially designed for children aged 7–11 years; however, further research has now extended its validity to children as young as 6 years⁵⁷ and in adolescents up to age 17 years.⁵⁸ The self-reported and proxy-reported versions of the CHU-9D questionnaire each consist of nine dimensions: sad, worried, annoyed, tired, sleep, pain, school, routine and activity. Each dimension contains five severity levels, resulting in almost two million unique health states associated with the measure. Responses from the CHU-9D instrument are transformed into QoL (utility) weights derived from a UK general population sample using an algorithm developed by Stevens.⁵⁹ This gives a possible utility value set of between 0.33 (the worst health state) and 1 (the best health state).

The PedsQL Generic Core Scale is a well-validated non-preference-based measure. The self-reported version of the questionnaire has been validated in 5- to 18-year-olds, whereas the parent- or proxy-reported version is valid for use in 2- to 18-year-olds. Both versions of the instrument comprise 20 questions across four subscales or domains of health. There is a different PedsQL module for toddlers (aged 2–4 years), young children (aged 5–7 years), older children (aged 8–12 years) and adolescents (aged 13–18 years). The number of items within the health domain varies in some modules based on age of the respondent. The physical functioning domain has eight items, and both the emotional functioning and the social functioning domains have five items each. School functioning has five items for all age groups except toddlers, for whom there are only three items. Similar to the CHU-9D instrument, responses to each of the 23 items are on a five-point scale of increasing severity: never a problem, almost never a problem, sometimes a problem, often a problem and almost always a problem. Total scores are on a 0–100 scale, with 100 reflecting best-possible health state.

Data

In accordance with the study protocol, the proxy-reported version of the PedsQL and the CHU-9D questionnaires were used to collect HRQoL data at weeks 4 (baseline) and 16, and at months 12, 24, 36 and 48 for participants in both treatment groups. PedsQL was completed for participants across all the age groups in the trial (2–18 years), with the appropriate age-specific module for the instrument applied, whereas the CHU-9D questionnaire was completed only for participants who were aged ≥ 5 years. Data on participants who had completed both instruments across all the time points were considered relevant for the mapping exercise. In order to optimise the sample size, the data for this eligible cohort for the five time points in the RCT were combined and randomised into groups A and B. Observations with valid CHU-9D and PedsQL index scores, that is, after excluding missing items, in groups A and B will from here on be referred to as the estimation sample and the validation sample, respectively. Together, the two samples form the total mapping sample.

Model specification

First, to assess the conceptual overlap between the two instruments across the whole sample, the interdimensional correlations between the nine CHU-9D and the four PedsQL domains were explored using Spearman’s correlation. Next, the prediction mapping exercise involved regressing the CHU-9D utility scores (independent variable) against the PedsQL total, subscale or item scores (dependent variables) to generate an algorithm that could be subsequently used to predict the CHU-9D values. In order to select the model with the best goodness-of-fit statistic, three ‘functional forms’ were explored. The first was the ordinary least squares (OLS) regression with predicted utility scores censored at the value of 1. Although the OLS regression minimises the sum of squared errors, and represents the most common method within mapping studies,⁶⁰ it has been shown that it does not cope well with multimodal distributions⁶¹ and does not always predict perfect health. The second was the generalised linear model (GLM),⁶² as it accommodates skewness in the estimation sample. The GLM requires specification of a distribution ‘family’ that captures the relationship between the mean and variance, and a link function between the linear part and the mean. The Modified Park test was applied to identify the preferred ‘family’ based on the lowest chi-squared value. The Hosmer–Lemeshow and Pearson correlation tests^63,64 were used to select the link function, assumed as a good fit if both tests yielded non-significant p-values. The third form chosen for the prediction function was the tobit model, a censored regression that accommodates both the lower and upper limit utility scores.⁶⁵ Tobit models have been suggested for mapping despite concerns about inconsistencies in the presence of non-normality and heteroscedasticity.⁶⁶ In summary, six model specifications (covariates) were developed based on the OLS, tobit and the GLM ‘functional forms’, thus generating 18 models in total:

• model 1 – PedsQL total scale score
• model 2 – model 1, age, and sex
• model 3 – PedsQL subscale scores
• model 4 – model 3, age and sex
• model 5 – PedsQL subscale score square terms and interaction terms
• model 6 – model 5, age and sex.

The PREDNOS data are a longitudinal data set that can be viewed as having a two-level structure, for which the data collection time points (level 1 units) are nested within participants (level 2 unit). Random intercept mixed-effect models are often used to account for this hierarchical data structure, but this was not considered appropriate in this context because, for mapping purposes, the error variance was expected to be constant over time: the CHU-9D and the PedsQL data were collected from each individual at discrete time points and any variance in the estimation error over time was, therefore, assumed to be constant. In line with the assumption of constant variance over time, the PREDNOS data were considered to have only one hierarchical level, which is at the participant level. The within-participant correlation was taken into account by including the ‘clustering’ option for each of the 18 model specifications. For example, the model 1 specification was:

where [participant ID] was a unique participant identifier.

Assessing model performance

The following selection criteria were applied to assess the estimation performance of the models:⁶⁷

• Step 1. The models were assessed on the exactness of the predicted mean value in the estimation sample.
• Step 2. One model from each functional form was selected based on its prediction accuracy in the estimation and validation sample. The indicators of prediction accuracy were the mean absolute error (MAE) and the mean squared error (MSE). The MAE is the mean absolute difference between the observed and the predicted values, while MSE is the mean squared difference between the observed and the predicted CHU-9D utility score. Larger MAE and MSE indicate poorer fit. MAE was prioritised over MSE, which has been shown to be less sensitive to outliers often found within the utility data.⁶⁸
• Step 3. To assess and compare the shortlisted models estimated in step 2, a number of criteria were considered:
  • The distribution of the predicted and the observed CHU-9D scores were plotted to examine how well the predicted scores matched the observed scores.
  • The proportion of predictions deviating from observed values by < 0.03, < 0.05 and < 0.1 were calculated as a representation of how often the models produce reliable predictions.
  • The MAEs were presented for different CHU-9D value ranges to assess how well the models perform at the top and bottom of the index score range.

All of the analysis described follows the MApping onto Preference-based measures reporting Standards (MAPS).⁶⁹

Sample characteristics

There were 643 observations across the five data collection time points from participants who were aged ≥ 5 years. These observations were randomised into groups A (n = 321) and B (n = 322). The longitudinal nature of the study meant that the number of missing data in the groups varied across the data collection points. After removing missing items, 279 observations with pairs of valid PedsQL and CHU-9D index scores in the first group formed the estimation sample, while the 284 observations in the second group formed the validation sample. The estimation and validation samples constitute the total mapping sample (n = 563). Figure 14 shows the distribution of the CHU-9D and PedsQL scores in the estimation and validation samples.

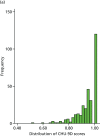
FIGURE 14

Distribution of CHU-9D and PedsQL scores in the estimation and validation samples. (a) Estimation sample, CHU-9D; (b) validation sample, CHU-9D; (c) estimation sample, PedsQL; and (d) validation sample, PedsQL.

Table 8 reports the descriptive statistics for each sample at each time point. Overall, it seems that the randomisation ensured a balanced distribution of demographic characteristics between the estimation and the validation samples.

TABLE 8

Demographic characteristics of estimation and validation sample by data collection time point

The mean CHU-9D utility score across all time points was 0.9374 (SD 0.0790) and 0.9409 (SD 0.0717) in the estimation and validation samples, respectively. The corresponding mean PedsQL score across all time points was 80.93 (SD 16.76) in the estimation sample and 80.31 (SD 17.79) in the validation sample. Within each sample, the mean PedsQL total score was lower than the mean CHU-9D utility score when both scores were standardised on a 100-point scale. Although both HRQoL measures were negatively skewed, the ceiling effect was more prominent with CHU-9D. Tables 23 and 24 in Appendix 3 summarise the CHU-9D responses for the estimation and validation samples across all data collection time points. Level 1 or ‘no problem’ always had the highest proportion of responses, hence the observed ceiling effect for the CHU-9D index score.

Performance and validation

Table 25 in Appendix 3 summarises the performance measures for all the model specifications, for both the estimation and the validation samples. Within the estimation sample, the models were able to reasonably predict the mean CHU-9D value (0.93742, SD 0.07898). Of the 18 models, 12 were able to predict the precise mean value by up to 1/10,000th of a QALY. The exceptions were the six tobit models. However, within the validation sample, the models were less able to predict the mean CHU-9D value (0.94094, SD 0.07174). The model GLM 2 had lowest mean predicted value (0.93409), whereas the model Tobit_3 had the highest mean predicted value (0.96575), giving a difference between the observed and predicted mean values of 0.0069 and 0.0245, respectively. These differences were below the threshold of 0.03, for which differences smaller than this level are considered to be a minimally important difference.^70,71 A further observation was that some OLS models and all the tobit models had maximum predicted values beyond the upper limit of the CHU-9D utility scale (0.33–1.00). However, none of the models predicted a utility value below the lower limit of the CHU-9D utility scale.

Models were initially assessed in terms of their ability to predict the mean value in the estimation sample. All GLM and OLS models were consequently shortlisted for further comparison and progress to ‘step 2’. The two models (GLM 6 and OLS 3) that had the ‘best’ performance in terms of MAE, in both the estimation and validation samples, were selected for a final comparison: ‘step 3’. Table 9 contains the model performance results for both of these models.

TABLE 9

Model performance of the two best-fitting models

For the GLM, a logit transformation of the variable containing the CHU-9D utility scores was applied before the variable was used as the dependent in the prediction equation. As such, any predicted value from that equation will be a transformed value and, therefore, requires a back-transformation to estimate utility values. The information on the back-transformation step is as follows. Given that GLM 6 has a logit link, the CHU-9D utility values are calculated as shown below:

For the final models in step 3, in addition to assessing how accurately the models estimated the mean CHU-9D score in the validation sample, the distribution of the predicted score was also examined (see Figure 17, Appendix 3). GLM 6 had a wide range of predicted CHU-9D scores compared with OLS 3.

Approximately 56% of the predicted values from GLM model 6 in the validation sample had absolute errors less than the minimally important difference value of 0.03; the corresponding values for the OLS model 3 was 53%. GLM model 6 remained the preferred model specification when the error threshold was extended to 0.05.

Although the prediction accuracy of the mean scores was similar in both models, the accuracy level was not uniform across the CHU-9D utility range, as shown in Table 10. The number of observations with utility score of < 0.7 was small; therefore, the comparison between the best two models was restricted to observations with higher utility values. GLM 6 was superior to OLS 3 in the estimation sample; however, in the validation sample there were diverging results. OLS 3 had a better prediction accuracy when utility values were > 0.8, but less than full health, while the GLM 6 was superior at predicting full health and utility values between 0.7 and 0.8. So, although OLS 3 had a better prediction accuracy in the validation sample overall, it was found to be only marginally better than GLM 6.

TABLE 10

Distribution of errors by observed CHU-9D range

In summary, relative to GLM 6, OLS 3 lacked the ability to predict the wider range of CHU-9D values (0.7–1), and a higher proportion of its predicted values had absolute errors above the minimally important difference. Furthermore, it was less able to predict full health, which is particularly important for utility data that tend to have ceiling effects. Taking all these factors into account, the GLM 6 model was selected as the preferred model for mapping from PedsQL to CHU-9D. Table 11 shows the coefficients for generating deterministic and probabilistic utility predictions using the GLM 6 model. Coefficients for OLS 3 have also been presented in situations in which this might be desired.

TABLE 11

Coefficients for the two best-fitting models