NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.
Crawford F, Chappell FM, Lewsey J, et al. Risk assessments and structured care interventions for prevention of foot ulceration in diabetes: development and validation of a prognostic model. Southampton (UK): NIHR Journals Library; 2020 Nov. (Health Technology Assessment, No. 24.62.)

Risk assessments and structured care interventions for prevention of foot ulceration in diabetes: development and validation of a prognostic model.
Show detailsIntroduction
A CPR is a way of presenting a statistical model that facilitates predictions that inform clinical decision-making. Statistical models can be unwieldy; they may have many predictors or predictors requiring transformation from their original scale, which can be off-putting to end-users and increase the scope for human error. In addition, the type of statistical model that is used for prediction is generally either a logistic regression model or a Cox proportional hazards model. These two models can be used to investigate the relationship between predictors and a binary or a categorical outcome (logistic regression) or the time until a binary outcome occurs (Cox proportional hazards model). Both types of statistical model require the use of a calculator, or similar, to make a prediction for an individual patient, as the estimate requires taking an exponential.
This chapter describes how we developed a statistical model for the prediction of DFU, used this model to create a simple-to-use CPR and validated the CPR in a data set not used in the development phase. We used the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) statement as a framework for reporting (see Appendix 3, Table 41).19
Clinical prediction rules can be presented simply as a regression equation, a nomogram or a scoring system; other formats are also possible. Whichever format is chosen, it should be remembered that the CPR is only as good as its underlying statistical model; therefore, the methodological requirements for good practice when building and validating a statistical model apply equally to CPRs. In addition, the presentation of a CPR can affect its acceptability to end-users. Our aim was to produce a CPR that does not require a calculator and is simple enough to be of very little burden in a busy clinic.
The benefit of a CPR is based not only on ease of use, but also, for example, on whether or not it provides useful information not otherwise available: will it improve patient outcomes and are there other ways to predict foot ulcer? The burden and sequelae of DFU to patients and the NHS are immense, so there is enormous interest in predicting which patients will develop ulceration. Therefore, it is unsurprising that we are not the first to attempt to make the prediction of ulcer easier for health professionals working directly with patients. This project, PODUS 2020, is a development of the work conducted in PODUS 2015, a SR and meta-analysis of IPD,15 in which we used the PODUS data sets to calculate ORs to quantify the association between risk categories, based on the recommendations of the International Working Group on Diabetic Foot (IWGDF), NICE and SIGN, and foot ulcer, as these are the guidelines likely to be used in the UK. The guidelines did not produce ORs that were significantly different from those obtained using insensitivity to monofilament only. Our final PODUS 2020 prediction model is simpler than current guidelines as it has only three predictors; it also includes insensitivity to monofilament. We knew, therefore, that we could use the PODUS data to develop and validate a simpler CPR that could perform at least as well as existing guidelines.
Methods
Source of data
The data for PODUS 2020 came from a previous research project, PODUS 2015 (see Appendix 3), published in the National Institute for Health Research (NIHR) Health Technology Assessment journal.15 PODUS 2015 obtained eight studies and had access to another two identified from an IPD SR. Eight studies contributed data to PODUS 2015.20–27 Access to a ninth study28 was available via a Safe Haven facility; a 10th study29 was not directly available but the PODUS 2015 team could request results of analyses from the data set. After the publication of PODUS 2015, we re-ran the searches to identify new studies and found only one that met the inclusion criteria. Unfortunately, the authors of that study did not respond to requests to share their data.30 The search strategy to find studies was last run in June 2017 for MEDLINE and in August 2017 for EMBASE, and was published as appendix 3 of the PODUS 2015 Health Technology Assessment journal publication.
Inclusion criteria for development and validation studies
Studies could be included in PODUS 2015 if patients had diabetes mellitus, predictors had been assessed at recruitment, foot ulcer status was assessed at follow-up and the study had recruited at least 100 patients. In addition, for a study to be included in PODUS 2020 development data sets, we required that it collected data on insensitivity to a 10-g monofilament, presence/absence of pedal pulses, history of ulceration or amputation, and the time period in which the ulcer occurs. As we planned to conduct a one-step meta-analysis at the development stage, we needed to merge all of the development data sets, and so required them to be stored on the same server. These criteria reduced the number of eligible development studies to four.20,21,24,25 Four studies did not provide data on sensitivity to monofilaments and/or the presence or absence of a pedal pulse,22,23,26,27 and the access arrangements for the Leese et al.28 and Boyko et al.29 data sets meant that they could not be stored on the same server as those of the other studies. The Boyko et al.29 data set had been used for validation in PODUS 2015, but included a very small proportion of women (< 2%). We therefore decided to use the Leese et al.28 data set for validation of the CPR.
We had no date restriction on studies. Recruitment dates ranged from 1 May 1995 to 10 November 2007 in the development data sets, and the final follow-up date was 5 December 2008. In the Leese et al.28 validation data set, recruitment dates ranged from 28 January 2001 to 8 December 2006 and the final follow-up date was 2007.
Critical appraisal of contributing studies
We used the Prediction model Risk Of Bias ASsessment Tool (PROBAST) tool to critically appraise the four validation studies and the external validation study.31 This was not used for PODUS 2015 because PODUS 2015 predated the publication of the PROBAST tool.
Participants
The four studies for development in PODUS 2020 comprised two studies set in the community in the UK and two hospital-based studies: one in mainland Europe and one in the USA. All studies recruited a consecutive sample. The Leese et al.28 data set used for validation is from another community-set study in the UK. The inclusion criteria for the data to be collected from each patient were as described in Inclusion criteria for development and validation studies; however, we also stipulated for both PODUS 2015 and PODUS 2020 that patients had to be aged ≥ 18 years and ulcer free at the time of recruitment. This meant that we had to remove from the analysis data set a small proportion of patients in some studies who had an ulcer at the time of recruitment. All studies were observational, and patients received the standard care in that setting.
Outcome
In PODUS 2020 we defined a binary outcome of presence or absence of foot ulceration within 2 years. Ulceration status was assessed by podiatrists (persons who diagnose and treat foot ailments; also known as chiropodists) or self-report questionnaires. We chose 2 years as the time interval as it is sufficient for an at-risk patient to develop an ulcer, it is clinically meaningful and it allowed us to use the largest study20 (> 6000 patients) that had defined the outcome as development of an ulcer by 2 years. The other three development data sets21,24,25 included either date of ulceration or time to ulceration, and, therefore, the data could be recoded to match the largest data set. However, we note that the planned length of follow-up in the Crawford et al.21 data set was only 1 year, and this was accounted for in our analyses. Assessment of outcome was, where possible, blinded to test results in three of the four development studies, but not in the Monteiro-Soares and Dinis-Ribeiro24 and Leese et al.28 validation study. It is, of course, not possible to blind podiatrists to previous amputations. As time to ulceration is also of interest, we conducted a survival analyses with the three studies with time-to-event data and present the results in Appendix 3.
Selection of predictors in PODUS 2020
In PODUS 2015, six predictors were selected from a potential candidate list of 22: age, sex, body mass index, smoking, height, weight, alcohol intake, glycated haemoglobin (HbA1c), insulin regime, duration of diabetes mellitus, eye problems, kidney problems, insensitivity to a 10-g monofilament, absence of pedal pulses, tuning fork, biothesiometer, ankle reflexes, ABI, peak plantar pressure, prior ulcer, prior amputation and foot deformity. Predictors were chosen for clinical plausibility, availability in at least three studies and lack of clinical heterogeneity. Statistical criteria such as small p-values were not used. Six variables were chosen for inclusion in the primary model in PODUS 2015: age, sex, duration of diabetes mellitus, insensitivity to a 10-g monofilament, absence of pedal pulses and prior ulcer or amputation. The analysis was a two-step meta-analysis. In each data set we fitted a logistic regression model with the six predictors, which gave us adjusted estimates for each predictor. We conducted a meta-analysis for each predictor using the generic inverse method.32 We had used a two-step method so that we could include, in the second stage, aggregate data (i.e. log-odds ratios and their variances) derived from the Leese et al.28 data set with > 3000 patients. The Leese et al.28 data set was housed on a different server and so could not be used in a one-step meta-analysis, although this is the preference of some methodologists.33
We tested these six predictors in the 10th, externally held data set,29 which had 1489 people and 229 ulcer outcomes. We considered the PODUS 2015 results to be replicated in the external data set if the predictor achieved statistical significance, if its effect was in the same direction as the PODUS 2015 estimate and if its CIs overlapped. The predictors that survived this process were insensitivity to a 10-g monofilament, absence of pedal pulses and prior ulcer or amputation.
For the CPR, we decided not to use the three predictors that were not replicated in the Boyko et al.29 data set: age, sex and duration of diabetes mellitus. Age and duration of diabetes mellitus are credible predictors of any diabetic complication, including foot ulcer. They are also continuous, which means that, in theory, they could be used to generate more precise risk estimates than categorical predictors; however, their inclusion in the CPR would require a calculator, or similar, to estimate risk. CPRs are a form of clinical decision support system that tend not to be used unless they are integrated into the existing workflow.34 The project did not have access to resources to support a website, or similar, that would calculate risk for health professionals or embed the CPR into NHS information technology systems. However, we could use three binary predictors that were replicated to produce a simple CPR that can be paper based and does not require any calculation from the users to implement. Practicalities as well as the lack of replication in the Boyko et al.29 data set were reasons to drop age and duration of diabetes mellitus from our CPR model; however, we understand that some individuals will be interested in the six predictor model, and the results from this model are in Appendix 3 and make direct comparisons with the three-predictor model. We also investigated possible reasons why age and duration of diabetes mellitus did not reach statistical significance or were not replicated predictors in the Boyko et al.29 data set. For simplicity, we also chose not to use the category sex as a predictor. Discussion with potential users of the CPR showed that they were very much in favour of a simpler model.
Definition of the PODUS 2020 predictors
We decided to use the three replicated predictors only (i.e. monofilaments, pulses and history) in the CPR. These three binary predictors were measured at the initial assessment of each patient in each study. In detail, the predictors are:
- Insensitivity to a 10-g monofilament at any site on either foot was defined as test positive. This test is carried out by podiatrists. The podiatrist touches the sole of the patient’s foot with a monofilament and the patient states whether or not he or she felt it.
- In general, there are two pulses tested in each foot: the dorsalis pedis and the posterior tibial pulses. We defined absence of either pulse on either foot as test positive, although it is known that the dorsalis pedis pulse is missing in some healthy individuals.35
- History of ulceration or amputation was ascertained either at initial assessment or from patient records. Patients were considered test positive for history if they had experienced either ulcer or amputation.
As predictors were measured before outcome in three of the four development studies, the measurement of predictors was blind to outcome. However, assessment of predictors blind to other predictors generally did not occur and would not always be possible; for example, toe amputation would be apparent to any podiatrist assessing monofilaments or pulses.
As in PODUS 2015, we chose to use patient rather than foot as the unit of analysis. The three binary predictors are defined as above, as this was the only way to have a consistent definition in all four development data sets; for example, Crawford et al.21 recorded the presence or absence of each of the four foot pulses, whereas Abbott et al.20 recorded the number of foot pulses per person (0–4). The outcome was binary and was defined as the occurrence or not of ulcer by 2 years.
In the PODUS 2015 publication, there is an extensive examination of differences and similarities between the studies as sources of heterogeneity.15 We repeat some of those analyses here to provide a description of the contributing data sets, with emphasis on the predictors chosen for PODUS 2020.
Sample size considerations
Sample size calculations are generally not carried out for meta-analyses conducted as part of a SR, as the aim is to use not an acceptable minimum but all of the available data. Post hoc sample size calculations are problematic and not recommended by statisticians, and so we did not conduct any.36 The development data sets have a total of 8255 people with 430 ulcer outcomes, giving 143 events per variable. This is well above the often-cited rule of thumb of 10 events per variable.37
Statistical models can often give overly optimistic results if the data from which they were derived come from small data sets, if data-driven methods are used to select variables or if too many variables are used. A way of compensating for optimistic results is to use a shrinkage factor:38 a number < 1 by which the coefficients are multiplied. All of the shrinkage factors that we calculated during the model development phase were > 0.9999, which would have resulted in negligible changes, so we did not use shrinkage factors. Shrinkage factors are affected by sample size and complexity of model but our model is simple and our sample size (events) is large relative to the number of included predictors.
The external validation data set had 3324 patients and 128 ulcer outcomes, meeting the recommendation of at least 100 events and 100 non-events to investigate model performance.39
Missing data
To account for missing data, we would have considered multiple imputation if we thought that data were likely to be missing at random (MAR).40 However, the proportion of missing data was very small (0–3% in the development data sets and < 2% in the largest data set of > 6000 patients) and so the results of any imputation exercise would not have made any notable difference to our results; therefore, we analysed the data using complete cases only, that is, patients for whom data on monofilaments, pulses, history and ulcer outcomes at 2 years were available.
One reason why outcome information at 2 years might be missing is death of the patient before 2 years. However, death was not consistently recorded across the data sets; for example, in the development studies, the largest study had recorded only one death in 2 years and another did not record deaths at all. The other two development studies were more systematic about including death data. Overall, the proportion of patients recorded as having died was 2%. If a patient had died, but had all information on predictors and outcome, that person was included in our analyses.
Some patients had missing data on previous amputation or ulcer history. However, the clinical context in which these data were collected means that it is very important to record when ulcers and amputations have occurred; therefore, the data were not MAR and are far more likely to be missing if the patients did not have previous ulcers and did not have amputations. Patients who were missing ulcer or amputation history were, therefore, recoded as test negative for these two items. The numbers of patients whose data were recoded are given in each study’s flow chart (Figures 1–4).

FIGURE 1
Flow of patients in the Abbott et al. data set. All patients had 2-year ulcer outcome recorded. Not all patients are shown at each stage.

FIGURE 4
Flow of patients in the Leese et al. study. Not all patients are shown at each stage.

FIGURE 2
Flow of patients in the Crawford et al. data set. Not all patients are shown at each stage.

FIGURE 3
Flow of patients in the Pham et al. study. Not all patients are shown at each stage.
Length of follow-up in the Crawford et al.21 data set
The PODUS 2020 outcome variable is ulcer occurrence by 2 years, and we knew that the Crawford et al.21 study had prespecified the follow-up period to be 12 months. We received ethics approval from the Scotland A Research Ethics Committee (reference 16/SS/0213: Integrated Research Approval System project ID 97542), Caldicott approval from NHS Tayside (reference IGTCAL3842) and NHS Tayside approval (reference 2017DM03, NHS Research Scotland reference NRS17/9754) for permission to contact the participants in the study by Crawford et al.21 to ask if they would consent to include longer-term data in PODUS 2020, some of which were stored on paper records. Despite all these efforts, follow-up data were obtained from only 42% of the original sample (see Appendix 3, Figure 33). Efforts were hampered by the non-retention of patient records for more than 8 years post death, patients being uncontactable and patients who did not consent. The PODUS 2020 Steering Committee discussed this issue and recommended that the data should not be used for the current project.
Analysis
Statistical analysis methods: choice of model
Given a binary outcome, the obvious method of analysis is logistic regression. Although other methods are available, we chose to base the CPR on a logistic regression model because this model is simple to implement and acceptable to the medical community, and the methods for assessing its performance are well developed. The selection of predictors was described in Definition of the PODUS 2020 predictors. We did not consider adding any interaction terms as these often do not improve the predictive ability of the model19 and would have made the CPR more complex.
As the data came from four studies, we used logistic regression with a separate intercept for each study to allow for clustering of participants within studies and to allow for between-study variation in baseline risk. This was especially important because of the inclusion of the Crawford et al.21 study, which had a follow-up duration of only 1 year, compared with 2 years in the other three studies. Although ORs of included predictors were similar in studies with 1- and 2-year’ follow-up, the baseline risk was not comparable, as it was higher in those studies with 2-year’ follow-up because of the longer time period.
For defining the intercept for our final CPR based on this logistic regression model, we chose a weighted average of the intercept estimates from the three studies with 2-year follow-up. This weighted average was obtained by using a random-effects meta-analysis of the three intercepts, and fitting using the DerSimonian and Laird method, which allows for both within-study variability (i.e. variance of intercept estimates) and between-study heterogeneity (i.e. genuine differences in baseline risk across studies beyond chance) (see Appendix 3, Figure 42). Therefore, the intercept in our final CPR model was not based on the Crawford et al.21 study (because of its 1-year follow-up), but predictor effects were based on the four developmental studies.
Statistical analysis methods: transformation of the logistic regression model into a clinical prediction rule
We adapted the method described by Steyerberg41 to generate a CPR from our logistic regression analyses. In brief, Steyerberg’s method is (1) multiply and round regression coefficients, (2) search scores for continuous predictors, (3) estimate the multiplication factor for the scores and (4) estimate the intercept and present a score chart. We omitted the second step because we had no continuous predictors and the third because our multiplication factor was 1. Steyerberg’s method could be applied to many different kinds of statistical model. We made a further modification to allow for the effect of the non-linear logit function used in logistic regression.
The outcome variable in binary logistic regression is the natural logarithm of the odds, or log-odds, of the binary event occurring:
where βs are log-odds ratios and the xs are the predictors. The intercept is the log-odds of the outcome occurring when all the predictors are zero. The probability of the outcome occurring can be calculated from the log-odds. For each unit change in x, the log-odds will increase by the corresponding β (a fixed amount), but the effect on the probability of outcome is not fixed because of the non-linear nature of the log-odds; for example, if the log-odds is 1.3, the corresponding probability is 78.6%. If the log-odds increases by 0.5 to 1.8, the probability becomes 85.8%, an increase in probability of 7.2%. If the log-odds is 2.3 and it is increased again by 0.5 to 2.8, the probability changes from 90.9% to 94.3%, an increase in probability of 3.4%, less than half the change before. The same change in log-odds does not mean the same change in probability given different values of initial log-odds; therefore, when considering the transformation of the logistic regression model into a simpler CPR, we also took account of the probabilities that would result from the scoring system as well as the size of the coefficients. This process was greatly simplified by having only three binary predictors. The number of possible predictor combinations is only eight, and it is not onerous to calculate the probability of ulcer for each combination.
To be explicit, our method was as follows:
- Fit the logistic regression model with the three risk factor predictors (monofilament, pulses and history) and study. This gives coefficients showing the extent to which the log-odds change for patients who have a test-positive result for monofilaments, pulses or history in comparison with lower-risk test-negative patients. There are also individual estimates for the intercept for each study. The intercept is the baseline risk of ulcer on the log-odds scale. We used SAS® PROC LOGISTIC (SAS Institute Inc., Cary, NC, USA; SAS and all other SAS Institute Inc. product or service names are registered trademarks or trademarks of SAS Institute Inc. in the US and other countries. ® indicates USA registration) with maximum likelihood estimation.
- Conduct a random-effects meta-analysis of the three intercepts from the studies with 2-year follow-up to get a single average intercept.
- Use this average intercept and the log-odds coefficients for the three predictors to calculate the probability of ulcer for each possible predictor combination; as there are three binary predictors, there are eight combinations.
- Multiply and round the coefficients of the predictors to get a CPR scoring scheme, bearing in mind that we wanted predictor combinations with similar probabilities of ulcer to have the same score.
- Repeat step 1 and step 2 using only the CPR score instead of monofilaments, pulses and history.
- Calculate the probability of ulcer for each score using a population average method.
In the case of a patient who has already contributed to one of the four development data sets, the most accurate estimate of baseline risk will be the appropriate study-specific intercept. A common way to estimate baseline risk for patients not recruited to the development data sets is simply to use the average intercept; however, our preference is to use the population average intercept method described by Pavlou et al.42 to get estimates of ulcer risk that are applicable to patients in new studies.
Validation of the clinical prediction rule
We assessed the internal validity of the CPR by examining its discrimination and calibration. Discrimination addresses how well the model’s predicted risks discriminate between those who will and those who will not develop an ulcer, and the calibration of how well the estimated risk matches the actual risk of ulceration. We used receiver operating characteristic (ROC) plots and the area under the ROC curve as a statistic of discrimination; the latter is also known as a c-statistic. We assessed calibration with calibration plots, estimation of the calibration slope, and calibration in the large. We assessed the external validity of the CPR in the Leese et al.28 data set again by examining the discrimination and calibration in the same way. For the validity analyses, we used the probability of ulcer as estimated by the CPR score and compared it with actual ulcer outcome at 2 years.
Other methods of assessing model performance in terms of clinical benefit are available, such as net benefit and decision curves, but we also noted that the performance of the CPR would be addressed using a health economic model.
Using discrimination and calibration statistics in both the development data sets and the Leese et al.28 validation data set aids comparison of the internal and external validity of the CPR. Exploratory analyses of all the data sets and investigation of heterogeneity was part of PODUS 2015. Hence we knew that the Leese et al.28 data set was broadly similar to the other data sets. In fact, there was an overlap of patients recruited to the Crawford et al.21 and Leese et al.28 data sets, and so we had to remove some patients from the Leese data set to avoid duplication of data. Relevant tables are in Results.
We have also included a net benefit graph to assess potential clinical impact.43 All analyses were conducted with SAS 9.4 [URL: www.sas.com (accessed 19 February 2019)] and R 3.4.2 [URL: https://cran.r-project.org/ (accessed 19 February 2019)]. The pROC,44 meta32 and rms45 packages in R statistical software (The R Foundation for Statistical Computing, Vienna, Austria) were used.
Results
Description of the individual studies
The quality of the cohort studies used to create the PODUS CPR is detailed in Table 1.31
TABLE 1
The risk-of-bias results for the PODUS studies
The flow of patients in the Abbott et al.20 data set is shown in Figure 1. The 38 patients with a history of amputation or ulcer and the 23 patients with a history of neither were coded accordingly. Thus, the number of complete cases was 6417 (97%) when recoded ulcer and amputation history was excluded and 6478 (98%) when it was included. One death was recorded in the study, but this patient was also missing pulses and so could not have been included in the development data set.
The number of complete cases in the Crawford et al.21 data set was 1175 (98.5%), as 18 patients were dropped from the analysis because information on monofilament sensitivity was absent and a further five were dropped because no follow-up time was provided and so ulcer occurrence by 2 years could not be calculated. There were 59 deaths in total in the Crawford et al.21 data set.
All of the variables required by the CPR were fully recorded in the Monteiro-Soares and Dinis-Ribeiro24 (n = 360) study and so we did not create a flow diagram. As the study setting was secondary care, these data are likely to be accurate. Some other data were missing in the Monteiro-Soares and Dinis-Ribeiro24 study, for example 189 (53%) patients were missing vibration perception threshold (VPT) data, but these were not required for the CPR. Deaths were not recorded.
In the Pham et al.25 study, the number of complete cases was 242 (97.6%). Three patients were missing a monofilament measurement and three had no time to ulcer/end of follow-up. One patient with a negative amputation history but no ulcer history was coded as negative for history. There were 13 deaths in the Pham et al.25 study.
The total number of patients in the development data sets was 8404 and the total number who contributed to the analyses was 8255, an overall rate of complete data of 98%.
Among the Leese et al.28 data set, 295 patients were removed from the analysis as they were included in the Crawford et al.21 data set. The Crawford et al.21 and Leese et al.28 studies recruited in a similar time period in overlapping geographical areas; however, we used the Scottish NHS patient identifier, the Community Health Index number46 (URL: www.ndc.scot.nhs.uk/Dictionary-A-Z/Definitions/index.asp?ID=128%26Title=CHI%20Number), to remove Crawford et al.21 patients from the Leese et al.28 data set. This reduced the size of the Leese et al.28 data set from 3707 to 3412 patients.
The percentage of complete cases in the Leese et al.28 data set was 97.4%; again, we considered this high enough not to require multiple imputation. During the follow-up period, 95 patients died.
We calculated summary statistics for all the predictors considered for the primary analysis of PODUS 2015, while noting that there is an extensive description of all the data sets in the PODUS 2015 publication.15
Summary statistics for age, duration of diabetes mellitus, sex, length of follow-up, sensitivity to monofilaments, absent pulses, history of amputation or ulceration and the results of outcomes (ulcer) are in Tables 2–9.
TABLE 2
Summary statistics for age for each development study, all of the development data sets and the Leese et al. validation data set
TABLE 9
Summary statistics for results for ulcer outcome by 2 years for each development study, all of the development data sets and the Leese et al. validation data set
TABLE 3
Summary statistics for known duration of diabetes mellitus (years) for each development study, all of the development data sets and the Leese et al. validation data set
TABLE 4
Summary statistics for sex for each development study, all of the development data sets and the Leese et al. validation data set
TABLE 5
Summary statistics for length of follow-up (months) for each development study and all of the development data sets
TABLE 6
Summary statistics for sensitivity/insensitivity to 1-g monofilament testing for each development study, all of the development data sets and the Leese et al. validation data set
TABLE 7
Summary statistics for pulses testing for each development study, all of the development data sets and the Leese et al. validation data set
TABLE 8
Summary statistics for history of amputation or ulceration for each development study, all of the development data sets and the Leese et al. validation data set
Although the Leese et al.28 study recorded patients’ test dates, in the case of occurrence only the year was recorded. Therefore, for this data set, we recorded an ulcer as having occurred within 2 years if one was recorded within 2 years of the year that the patient was first seen. This is not a precise way of coding ulcer outcome by 2 years, but it allowed us to use the data set. Ulcer outcomes were recorded from 2001 to 2007; the median year of occurrence was 2005.
From the coding detailed above, the total number of patients from the development data sets used in the logistic regression model underlying the CPR was 8255 (98%), of whom 430 had ulcer-positive outcomes and 7825 had ulcer-negative outcomes at 2 years. In the Leese et al.28 validation data set 3324 patients had suitable data, of whom 128 had an ulcer by 2 years and 3196 did not. We did not compute unadjusted ORs for the predictor and outcome, as this work had already been done as part of PODUS 2015.15
Development and testing of the clinical prediction rule: initial logistic regression model and random-effects meta-analysis
As outlined in Statistical analysis methods: transformation of the logistic regression model into a clinical prediction rule, the results of steps 1 and 2 of building the CPR are presented here.
On the log-odds scale, the initial logistic regression model with original predictors (coded 0 if test negative and 1 if test positive) was:
The intercept of –3.81 was taken from a random-effects meta-analysis of the intercepts of the three studies with 2-year follow-up data.
Calculating probability of ulcer for each predictor combination
We used Equation 2 to carry out step 3 of the CPR building by first calculating the log-odds of ulcer for each prediction combination and then converting that log-odds to a probability.
Generating a scoring scheme
Part of step 4 was examining ulcer risk probabilities (Table 10). This showed that some different predictor combinations had similar risk. For example, we wanted the (0,0,1) predictor combination with a probability of 0.134 to have the same score as the (1,1,0) combination with a probability of 0.118. Using the probabilities and the method of multiplying and rounding the predictor coefficients described by Steyerberg,41 the CPR scoring method is:
TABLE 10
Probability of ulcer for each of the eight predictor combinations
- score 1 if patient is insensitive to monofilaments
- score 1 if patient is missing any pulse
- score 2 if patient has a history of ulcer or amputation.
This results in a CPR that gives scores from 0 to 4. We calculated this score for each patient and refitted the logistic regression model using CPR score as the only predictor.
Refitting the logistic regression model with clinical prediction rule score as the only predictor
The resulting logistic regression model from steps 4 and 5 in Statistical analysis methods: transformation of the logistic regression model into a clinical prediction rule using CPR score is:
The intercept again was taken from a random-effects meta-analysis of the intercepts of the three studies with 2-year follow-up data. We did not use this formula to calculate the probability of an ulcer, but, if we had decided to, the corresponding formula for probability would be:
Using Equation 4 would be perfectly acceptable, but we could calculate population-averaged probabilities of ulcer, which should be generalisable to new studies. The formula for doing so is complex, and not something that can be done easily without statistical software.42 We therefore calculated the probabilities for our end-users, as one of our aims is that our CPR be easy to use. This is the sixth and final step outlined in Statistical analysis methods: transformation of the logistic regression model into a clinical prediction rule.
Internal validity of the clinical prediction rule
The calibration of the CPR is shown in Figure 5 (using the study-specific estimates) and in Figure 6 (using the population average estimates). The study-specific estimates, by definition, have a calibration slope of 1 and an intercept of 0, showing that the model has ideal calibration in the data set in which it was developed. The changes in slope and intercept for the population average estimates show that the CPR has been slightly recalibrated. We show these graphs for comparison with the calibration plot obtained with the Leese et al.28 validation data set and because external calibration is a better guide of how a model will perform than internal calibration.
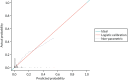
FIGURE 5
Calibration plot for the CPR using study-specific estimates from the development data sets.
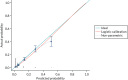
FIGURE 6
Calibration plot for the CPR using population average estimates from the development studies.
Discrimination of the CPR shown in Table 11 was assessed by calculating the area under the ROC curve (Figure 7). The c-statistic for the CPR is 0.796 (95% CI 0.772 to 0.820) and for the three-predictor model (monofilaments, pulses and history) is 0.802 (95% CI 0.778 to 0.825).
TABLE 11
Population-based probability of ulcer at 2 years for each CPR score, calculated using Pavlou’s method for population average estimates in the development data sets
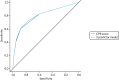
FIGURE 7
The ROC curves for the CPR and three-predictor model for the prediction of ulcer at 2 years derived from the development data sets.
External validity of the clinical prediction rule
The discrimination and calibration plots generated by the CPR in the Leese et al.28 data set show very similar results to those of the internal validation (Figures 8–10). Again, the calibration statistics suggest that the probability of ulcer at 2 years is underestimated by the CPR.

FIGURE 8
The external validation ROC plot from the Leese et al. data set.
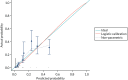
FIGURE 10
The external validation calibration plot from the Leese et al. data set for the three-predictor model.
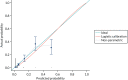
FIGURE 9
The external validation calibration plot from the Leese et al. data set for the CPR.
We also compared the performance of the CPR with that of the original three-predictor model and found very little loss of accuracy with the CPR (Table 12). Appendix 3 gives a further comparison of the three-predictor and score models, using the development data sets.
TABLE 12
External data calibration statistics for the three-predictor and CPR models
The c-statistic for the CPR is 0.829 (95% CI 0.790 to 0.868). The c-statistic for the three-predictor model is 0.834 (95% CI 0.794 to 0.873).
At a risk threshold of 6%, the net benefit is 0 for treat none and < 0 for treat all, but 0.015 for using the CPR (Figure 11). This can be interpreted as follows: if we choose to treat patients with CPR scores of ≥ 1, then, for every 1000 individuals, 15 additional cases of ulcer at 2 years would be correctly identified for treatment by the CPR, without increasing the number treated unnecessarily. At a risk threshold of 14%, the number of additional cases of ulcer at 2 years identified for treatment would be 10 per 1000 individuals.
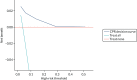
FIGURE 11
Net benefit plot for use of the CPR to identify patients who would benefit from an intervention to prevent foot ulcer, generated from the Leese et al. validation data set.
Table 13 shows the PODUS CPR that is designed to predict the risk of ulceration within 2 years of patients with diabetes mellitus who do not currently have a foot ulcer.
TABLE 13
Printable display version of the PODUS CPR
Discussion
The CPR is simple and can be used without a calculator. The elements of the scoring system comprise neurological damage, as assessed by sensitivity to a 10-g monofilament; vascular damage, as assessed by the presence or absence of pedal pulses; and propensity to ulcerate, as assessed by history. This will give the CPR face validity for end-users. Monofilament sensitivity and the presence of pulses are quick, simple and cheap to measure. History of ulcer or amputation should be noted in the patient’s records or identifiable from the patient’s presentation.
An important component in the development of complications in diabetes mellitus is self-care by patients. We have very few data on this in the PODUS data sets, and so the statistical model underlying our CPR is incomplete. This may be why the CPR underestimates risk as some of the risk of ulcer development will depend on the level of diabetic control achieved by the patient; however, how self-care should be measured is the subject of ongoing research.47
The performance of the CPR in the Leese et al.28 validation data set suggests that simplifying the three-predictor model into the CPR resulted in little loss of discrimination and calibration. The calibration graphs indicate that both the CPR and the three-predictor model are least accurate for high-risk patients: those with a history of ulceration or amputation and at least one other risk factor. However, the treatment pathway for these patients is the same, so the use of neither the CPR nor the three-predictor model would result in a change in their care.
Ideally, the CPR will be validated in a new, prospective study. A new study’s results would be applicable to patients living with diabetes mellitus today. Although we made every reasonable effort to gather all of the data that were available, the data sets are not very recent and the factors driving the development of foot ulcer may have changed.
A small number of patients developed ulcers despite exhibiting no neurological or vascular damage (< 5% of all ulcers), but amputation is rarely necessary in such cases. The proportion of patients with this predictor combination was 1.96% in the development data sets and 0.93% in the validation data set.
- Clinical prediction rule: PODUS data - Risk assessments and structured care inte...Clinical prediction rule: PODUS data - Risk assessments and structured care interventions for prevention of foot ulceration in diabetes: development and validation of a prognostic model
- Discussion and conclusions - Strategies for older people living in care homes to...Discussion and conclusions - Strategies for older people living in care homes to prevent urinary tract infection: the StOP UTI realist synthesis
- Study design and methods - Improving the economic value of photographic screenin...Study design and methods - Improving the economic value of photographic screening for optical coherence tomography-detectable macular oedema: a prospective, multicentre, UK study
- Discussion - Validation and development of models using clinical, biochemical an...Discussion - Validation and development of models using clinical, biochemical and ultrasound markers for predicting pre-eclampsia: an individual participant data meta-analysis
- hypothetical protein AeMF1_009603 [Aphanomyces euteiches]hypothetical protein AeMF1_009603 [Aphanomyces euteiches]gi|2180795211|gb|KAH9116461.1||gnl| AJNMJ|cds.AeMF1_9647.1Protein
Your browsing activity is empty.
Activity recording is turned off.
See more...